Алгебра и начала анализа для учащихся 11 класса поурочные планы
рассмотреть решения более сложных упражнений на нахождение площади криволинейной трапеции; проверить степень усвоения этого материала - ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА - ИНТЕГРАЛ - 1-е полугодие
Цели: рассмотреть решения более сложных упражнений на нахождение площади криволинейной трапеции; проверить степень усвоения этого материала.
Ход урока
I. Проверка домашнего задания
Фронтально проверить решение домашнего задания. Ответить на вопросы учащихся.
II. Решение упражнений № 365 (б), № 366 (б), № 367.
№ 365 (б)
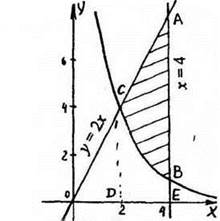
Рис. 13
Решение
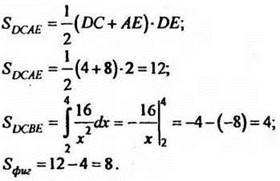
№ 366 (б)
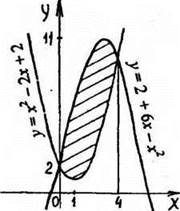
Рис. 14
Решение
Пределы интегрирования:
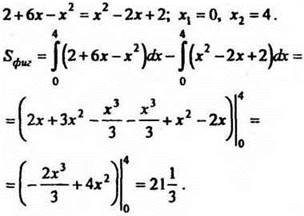
№ 367
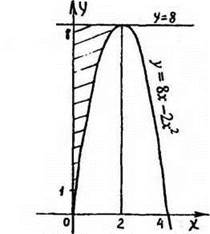
Рис. 15
Решение
1. Уравнение касательной:
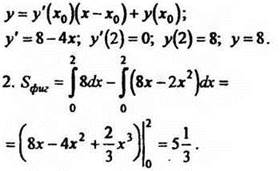
III. Самостоятельная работа (проверяется на этом же уроке с помощью шаблона) .
Вариант I
1. Вычислите интеграл 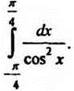 Ответ: 1) 1; 2) -3; 3) 0; 4) 2.
Ответ: 1) 1; 2) -3; 3) 0; 4) 2.
2. Вычислите интеграл 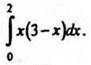 Ответ: 1) 10/3; 2) 26/3; 3) 6; 4) 8/3.
Ответ: 1) 10/3; 2) 26/3; 3) 6; 4) 8/3.
3. Вычислите площадь фигуры, ограниченной параболой у = 1 - х2 и осью ОХ. Ответ: 1) 2/3; 2) 8/3; 3) 4/3; 4) 1.
4. Вычислите площадь фигуры, ограниченной линиями y = sin2х; у = 0; х = 0 и х = ![]() /2. Ответ: 1) 2; 2) 1; 3) 1/2; 4) 3/2.
/2. Ответ: 1) 2; 2) 1; 3) 1/2; 4) 3/2.
Вариант II
1. Вычислите интеграл 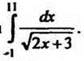 Ответ: 1) 4; 2) -3; 3) 3/2; 4) 7.
Ответ: 1) 4; 2) -3; 3) 3/2; 4) 7.
2. Вычислите интеграл 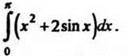
Ответ: 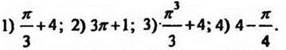
3. Вычислите площадь фигуры, ограниченной параболой у = 6(х - х2) и осью ОХ. Ответ: 1) 1/2; 2) 5 ; 3) 4; 4) 1.
4. Вычислите площадь фигуры, ограниченной линиями у = sin2x; y = 0; х = 0 и х = ![]() /4. Ответ: 1) 1; 2) 1/2; 3) 2; 4) 1,5.
/4. Ответ: 1) 1; 2) 1/2; 3) 2; 4) 1,5.
Вариант III
1. Вычислите интеграл 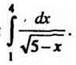 Ответ: 1) 12; 2) -2; 3) 2; 4) 6.
Ответ: 1) 12; 2) -2; 3) 2; 4) 6.
2. Вычислите интеграл 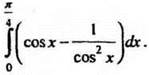 Ответ:
Ответ: ![]()
![]()
3. Вычислите площадь фигуры, ограниченной параболой у = 7х – х2 - 10 и осью ОХ. Ответ: 1) 14; 2) 64,5; 3) 4; 5) 4,5.
4. Вычислите площадь фигуры, ограниченной линиями y = cos2x; х = -![]() /4; х =
/4; х = ![]() /4 и у = 0. Ответ: 1) 1; 2) -1; 3) 1,5; 4) 2.
/4 и у = 0. Ответ: 1) 1; 2) -1; 3) 1,5; 4) 2.
Вариант IV (для сильных учащихся)
1. Вычислите интеграл 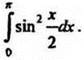 Ответ: 1) -1; 2)
Ответ: 1) -1; 2) ![]() /2 - 1; 3)
/2 - 1; 3) ![]() /2; 4) 1.
/2; 4) 1.
2. Вычислите интеграл 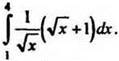 Ответ: 1) 5; 2) -5; 3) -3; 4) 7.
Ответ: 1) 5; 2) -5; 3) -3; 4) 7.
3. Вычислите площадь фигуры, ограниченной линией -х2 + 7|х| - 10 и осью ОХ. Ответ: 1) 26; 2) 8; 3) ![]() ; 4)
; 4) ![]() .
.
4. Вычислите площадь фигуры, ограниченной линиями ![]() Ответ: 1) -5/12; 2) 0,6; 3) 5/12; 4) 1/2.
Ответ: 1) -5/12; 2) 0,6; 3) 5/12; 4) 1/2.
IV. Итоги урока
V. Домашнее задание: п. 30; № 365 (а, г), № 366 (г). № 368; вспомнить примеры применения производной.
По желанию.
1. Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции ![]() в точке с абсциссой х0 = 1.
в точке с абсциссой х0 = 1.
Ответ: 2.
2. Вычислите площадь фигуры, ограниченной линиями х = 0, у = sin х, у = cosx, х = ![]() /2. Ответ:
/2. Ответ: ![]()