Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Системы тригонометрических уравнений (факультативное занятие) - Преобразование тригонометрических выражений - 2-е полугодие
Цель: рассмотреть наиболее типичные системы тригонометрических уравнений и способы их решения.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Решите неравенство:
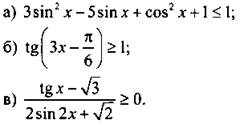
Вариант 2
Решите неравенство:
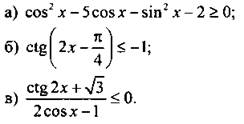
III. Изучение нового материала
На экзаменах системы тригонометрических уравнений встречаются гораздо реже тригонометрических уравнений и неравенств. Четкой классификации систем тригонометрических уравнений не существует. Поэтому условно разобьем их на группы и рассмотрим способы решения этих задач.
1. Простейшие системы уравнений
К ним отнесем системы, в которых или одно из уравнений является линейным, или уравнения системы могут быть решены независимо друг от друга.
Пример 1
Решим систему уравнений 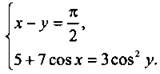
Так как первое уравнение является линейным, то выразим из него переменную ![]() и подставим во второе уравнение:
и подставим во второе уравнение: ![]() Используем формулу приведения и основное тригонометрическое тождество. Получим уравнение
Используем формулу приведения и основное тригонометрическое тождество. Получим уравнение ![]() или
или ![]() Введем новую переменную t = sin у. Имеем квадратное уравнение 3t2 - 7t + 2 = 0, корни которого t1 = 1/3 и t2 = 2 (не подходит, так как sin у ≤ 1). Вернемся к старой неизвестной и получим уравнение sin y = 1/3, решение которого
Введем новую переменную t = sin у. Имеем квадратное уравнение 3t2 - 7t + 2 = 0, корни которого t1 = 1/3 и t2 = 2 (не подходит, так как sin у ≤ 1). Вернемся к старой неизвестной и получим уравнение sin y = 1/3, решение которого ![]() Теперь легко найти неизвестную:
Теперь легко найти неизвестную: ![]() Итак, система уравнений имеет решения
Итак, система уравнений имеет решения ![]() где n ∈ Z.
где n ∈ Z.
Пример 2
Решим систему уравнений 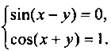
Уравнения системы независимы. Поэтому можно записать решения каждого уравнения. Получим: ![]() Почленно сложим и вычтем уравнения этой системы линейных уравнений и найдем:
Почленно сложим и вычтем уравнения этой системы линейных уравнений и найдем: ![]() откуда
откуда ![]()
Обратим внимание на то, что в силу независимости уравнений при нахождении х - у и х + у должны быть указаны разные целые числа n и k. Если бы вместо k было также поставлено n, то решения имели бы вид: ![]() При этом было бы потеряно бесконечное множество решений и, кроме того, возникла бы связь между переменными x и у: х = 3у (чего нет на самом деле). Например, легко проверить, что данная система имеет решение х = 5π и у = п (в соответствии с полученными формулами), которое при k = n найти невозможно. Поэтому будьте внимательнее.
При этом было бы потеряно бесконечное множество решений и, кроме того, возникла бы связь между переменными x и у: х = 3у (чего нет на самом деле). Например, легко проверить, что данная система имеет решение х = 5π и у = п (в соответствии с полученными формулами), которое при k = n найти невозможно. Поэтому будьте внимательнее.
2. Системы вида 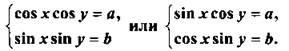
Такие системы приводятся к простейшим при сложении и вычитании уравнений. При этом получим системы 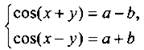 или
или 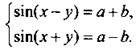 Отметим очевидное ограничение:
Отметим очевидное ограничение: ![]() и
и ![]() Само же решение подобных систем сложностей не представляет.
Само же решение подобных систем сложностей не представляет.
Пример 3
Решим систему уравнений 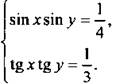
Преобразуем сначала второе уравнение системы, используя равенство ![]() Получим:
Получим: ![]() Подставим в числитель этой дроби первое уравнение:
Подставим в числитель этой дроби первое уравнение: 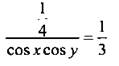 и выразим
и выразим ![]() Теперь имеем систему уравнений
Теперь имеем систему уравнений 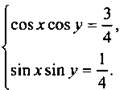 Сложим и вычтем эти уравнения. Имеем:
Сложим и вычтем эти уравнения. Имеем: 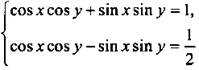 или
или 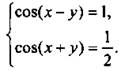 Запишем решения этой простейшей системы:
Запишем решения этой простейшей системы: 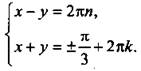 Складывая и вычитая эти линейные уравнения, находим:
Складывая и вычитая эти линейные уравнения, находим: ![]()
3. Системы вида 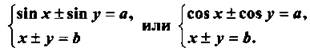
Такие системы можно рассматривать как простейшие и решать их соответствующим образом. Однако есть и другой способ решения: преобразовать сумму тригонометрических функций в произведение и использовать оставшееся уравнение.
Пример 4
Решим систему уравнений 
Сначала преобразуем первое уравнение, используя формулу для суммы синусов углов. Получим: ![]() Используя второе уравнение, имеем:
Используя второе уравнение, имеем:  откуда
откуда  Выпишем решения этого уравнения:
Выпишем решения этого уравнения: ![]() С учетом второго уравнения данной системы получаем систему линейных уравнений
С учетом второго уравнения данной системы получаем систему линейных уравнений 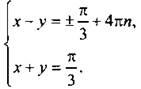 Из этой системы находим
Из этой системы находим  Такие решения удобно записать в более рациональном виде. Для верхних знаков имеем:
Такие решения удобно записать в более рациональном виде. Для верхних знаков имеем: ![]() для нижних знаков -
для нижних знаков - 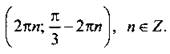
4. Системы вида 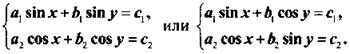
Прежде всего необходимо получить уравнение, содержащее только одну неизвестную. Для этого, например, выразим из одного уравнения sin у, из другого - cos у. Возведем в квадрат эти соотношения и сложим. Тогда получается тригонометрическое уравнение, содержащее неизвестную х. Решаем такое уравнение. Затем, используя любое уравнение данной системы, получаем уравнение для нахождения неизвестной у.
Пример 5
Решим систему уравнений ![]()
Запишем систему в виде 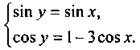 Возведем в квадрат каждое уравнение системы и получим:
Возведем в квадрат каждое уравнение системы и получим: 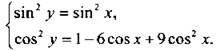 Сложим уравнения этой системы:
Сложим уравнения этой системы: ![]() или
или ![]() Используя основное тригонометрическое тождество, запишем уравнение в виде
Используя основное тригонометрическое тождество, запишем уравнение в виде ![]() или
или ![]() Решения этого уравнения cos x = 1/2 (тогда
Решения этого уравнения cos x = 1/2 (тогда ![]() ) и cos x = 1/4 (откуда
) и cos x = 1/4 (откуда ![]() ), где n, k ∈ Z. Учитывая связь между неизвестными cos y = 1 – 3 cos x, получим: для cos x = 1/2 cos y = -1/2; для cos x = 1/4 cos y = 1/4. Необходимо помнить, что при решении системы уравнений проводилось возведение в квадрат и эта операция могла привести к появлению посторонних корней. Поэтому надо учесть первое уравнение данной системы, из которого следует, что величины sin x и sin у должны быть одного знака.
), где n, k ∈ Z. Учитывая связь между неизвестными cos y = 1 – 3 cos x, получим: для cos x = 1/2 cos y = -1/2; для cos x = 1/4 cos y = 1/4. Необходимо помнить, что при решении системы уравнений проводилось возведение в квадрат и эта операция могла привести к появлению посторонних корней. Поэтому надо учесть первое уравнение данной системы, из которого следует, что величины sin x и sin у должны быть одного знака.
С учетом этого получим решения данной системы уравнений ![]() и
и ![]() где n, m, k, l ∈ Z. При этом для неизвестных х и у одновременно выбирают или верхние, или нижние знаки.
где n, m, k, l ∈ Z. При этом для неизвестных х и у одновременно выбирают или верхние, или нижние знаки.
В частном случае ![]() система может быть решена преобразованием суммы (или разности) тригонометрических функций в произведение и последующим почленным делением уравнений друг на друга.
система может быть решена преобразованием суммы (или разности) тригонометрических функций в произведение и последующим почленным делением уравнений друг на друга.
Пример 6
Решим систему уравнений 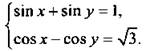
В каждом уравнении преобразуем сумму и разность функций в произведение и разделим каждое уравнение на 2. Получим:  Так как ни один множитель в левых частях уравнений не равен нулю, то почленно разделим уравнения друг на друга (например, второе на первое). Получим:
Так как ни один множитель в левых частях уравнений не равен нулю, то почленно разделим уравнения друг на друга (например, второе на первое). Получим: ![]() откуда
откуда ![]() Подставим найденное значение
Подставим найденное значение ![]() например, в первое уравнение:
например, в первое уравнение: ![]() Учтем, что
Учтем, что ![]() Тогда
Тогда ![]() откуда
откуда ![]()
Получили систему линейных уравнений 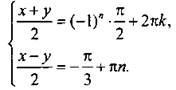 Складывая и вычитая уравнения этой системы, найдем
Складывая и вычитая уравнения этой системы, найдем ![]() и
и ![]() где n, k ∈ Z.
где n, k ∈ Z.
5. Системы, решаемые с помощью замены неизвестных
Если система содержит только две тригонометрические функции или приводится к такому виду, то удобно использовать замену неизвестных.
Пример 7
Решим систему уравнений 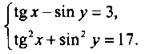
Так как в данную систему входят только две тригонометрические функции, то введем новые переменные а = tg х и b = sin у. Получим систему алгебраических уравнений 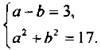 Из первого уравнения выразим а = b + 3 и подставим во второе:
Из первого уравнения выразим а = b + 3 и подставим во второе: ![]() или
или ![]() Корни этого квадратного уравнения b1 = 1 и b2 = -4. Соответствующие значения а1 = 4 и а2 = -1. Вернемся к старым неизвестным. Получим две системы простейших тригонометрических уравнений:
Корни этого квадратного уравнения b1 = 1 и b2 = -4. Соответствующие значения а1 = 4 и а2 = -1. Вернемся к старым неизвестным. Получим две системы простейших тригонометрических уравнений:
а) ![]() ее решение
ее решение ![]() где n, k ∈ Z.
где n, k ∈ Z.
б) ![]() решений не имеет, так как sin у ≥ -1.
решений не имеет, так как sin у ≥ -1.
Пример 8
Решим систему уравнений 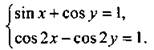
Преобразуем второе уравнение системы так, чтобы оно содержало только функции sin х и cos у. Для этого используем формулы понижения степени. Получим: ![]() (откуда
(откуда ![]() ) и
) и ![]() (тогда
(тогда ![]() ). Второе уравнение системы имеет вид:
). Второе уравнение системы имеет вид: ![]() или
или ![]() Получили систему тригонометрических уравнений
Получили систему тригонометрических уравнений 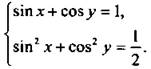 Введем новые переменные a = sin х и b = cos у. Имеем симметричную систему уравнений
Введем новые переменные a = sin х и b = cos у. Имеем симметричную систему уравнений 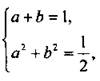 единственное решение которой a = b = 1/2. Вернемся к старым неизвестным и получим простейшую систему тригонометрических уравнений
единственное решение которой a = b = 1/2. Вернемся к старым неизвестным и получим простейшую систему тригонометрических уравнений 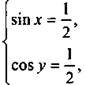 решение которой
решение которой 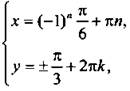 где n, k ∈ Z.
где n, k ∈ Z.
6. Системы, для которых важны особенности уравнений
Практически при решении любой системы уравнений используются те или иные ее особенности. В частности, один из наиболее общих приемов решения системы - тождественные преобразования, позволяющие получить уравнение, содержащее только одну неизвестную. Выбор преобразований, конечно, определяется спецификой уравнений системы.
Пример 9
Решим систему 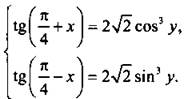
Обратим внимание на левые части уравнений, например на ![]() Используя формулы приведения, сделаем из нее функцию с аргументом π/4 + х. Получим:
Используя формулы приведения, сделаем из нее функцию с аргументом π/4 + х. Получим: ![]()
![]() Тогда система уравнений имеет вид:
Тогда система уравнений имеет вид: 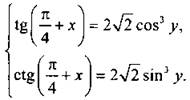 Чтобы исключить переменную х, почленно умножим уравнения и получим:
Чтобы исключить переменную х, почленно умножим уравнения и получим: ![]() или 1 = sin3 2у, откуда sin 2у = 1. Находим
или 1 = sin3 2у, откуда sin 2у = 1. Находим ![]() и
и ![]() Удобно отдельно рассмотреть случаи четных и нечетных значений n. Для четных n (n = 2k, где k ∈ Z)
Удобно отдельно рассмотреть случаи четных и нечетных значений n. Для четных n (n = 2k, где k ∈ Z) ![]() Тогда из первого уравнения данной системы получим:
Тогда из первого уравнения данной системы получим: ![]() где m ∈ Z. Для нечетных
где m ∈ Z. Для нечетных ![]() Тогда из первого уравнения имеем:
Тогда из первого уравнения имеем: ![]() Итак, данная система имеет решения
Итак, данная система имеет решения 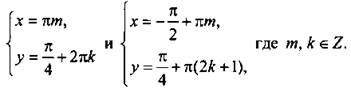
Как и в случае уравнений, достаточно часто встречаются системы уравнений, в которых существенную роль играет ограниченность функций синуса и косинуса.
Пример 10
Решим систему уравнений 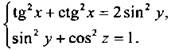
Прежде всего преобразуем первое уравнение системы: ![]() или
или ![]() или
или ![]() или
или ![]() или
или ![]() Учитывая ограниченность функции синуса, видим, что левая часть уравнения не меньше 2, а правая часть не больше 2. Поэтому такое уравнение равносильно условиям sin2 2х = 1 и sin2 у = 1.
Учитывая ограниченность функции синуса, видим, что левая часть уравнения не меньше 2, а правая часть не больше 2. Поэтому такое уравнение равносильно условиям sin2 2х = 1 и sin2 у = 1.
Второе уравнение системы запишем в виде sin2 у = 1 - cos2 z или sin2 у = sin2 z, и тогда sin2 z = 1. Получили систему простейших тригонометрических уравнений 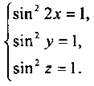 Используя формулу понижения степени, запишем систему в виде
Используя формулу понижения степени, запишем систему в виде 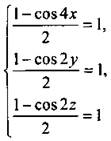 или
или 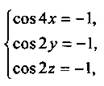 тогда
тогда 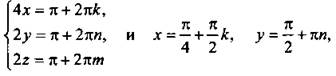
![]()
Разумеется, при решении других систем тригонометрических уравнений также необходимо обращать внимание на особенности этих уравнений.
7. Системы, содержащие обратные тригонометрические функции
Такие системы встречаются гораздо реже, чем системы уравнений с тригонометрическими функциями. Поэтому остановимся только на нескольких примерах и обратим внимание на особенности решения подобных систем.
Пример 11
Выясним, при каких целых значениях k система уравнений 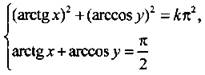 имеет решения, и найдем все эти решения,
имеет решения, и найдем все эти решения,
Так как в эту систему входят только две обратные тригонометрические функции, то введем новые переменные a = arctg х и b = arccos у. Тогда система имеет вид:  Найдем возможные значения k. Учитывая области изменения функций arctg х и arccos у, получим:
Найдем возможные значения k. Учитывая области изменения функций arctg х и arccos у, получим: ![]() Отсюда имеем:
Отсюда имеем: ![]() Сложив эти неравенства одного знака, получим:
Сложив эти неравенства одного знака, получим: ![]() Учитывая первое уравнение системы, получим:
Учитывая первое уравнение системы, получим: ![]() или
или ![]() В промежуток [0; 5/4) входят два целых значения k = 0 и k = 1. Рассмотрим два этих случая.
В промежуток [0; 5/4) входят два целых значения k = 0 и k = 1. Рассмотрим два этих случая.
а) При k = 0 система имеет вид: 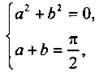 и решений не имеет.
и решений не имеет.
б) При k = 1 система принимает вид: 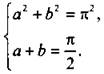 Из второго уравнения выразим b = π/2 - а и подставим в первое. Имеем:
Из второго уравнения выразим b = π/2 - а и подставим в первое. Имеем: ![]() или
или ![]() Корни этого квадратного уравнения
Корни этого квадратного уравнения 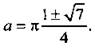 Очевидно, что корень
Очевидно, что корень 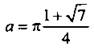 не подходит, так как
не подходит, так как 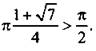 Для значения
Для значения 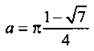 найдем
найдем ![]() (очевидно, что 0 ≤ b ≤ π). Вернемся к старым неизвестным и получим систему уравнений
(очевидно, что 0 ≤ b ≤ π). Вернемся к старым неизвестным и получим систему уравнений 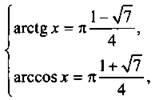 которая имеет единственное решение
которая имеет единственное решение 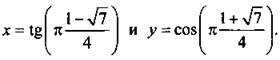
Итак, только при k = 1 данная система уравнений имеет единственное решение 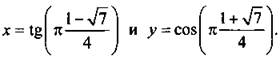
На экзаменах встречаются также системы уравнений, содержащие обратные и прямые тригонометрические функции. Рассмотрим пример такой смешанной системы.
Пример 12
Решим систему уравнений 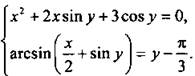
Учитывая область изменения функции арксинуса, из второго уравнения получим неравенство ![]() Откуда
Откуда ![]() По определению функции арксинуса из второго уравнения имеем:
По определению функции арксинуса из второго уравнения имеем: ![]() или
или ![]() или
или 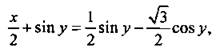 откуда выразим
откуда выразим ![]() Подставим это соотношение в первое уравнение данной системы. Получим:
Подставим это соотношение в первое уравнение данной системы. Получим: ![]() или
или ![]() Используя основное тригонометрическое тождество, имеем уравнение
Используя основное тригонометрическое тождество, имеем уравнение ![]() Решения этого уравнения cos y = -1 (тогда
Решения этого уравнения cos y = -1 (тогда ![]() ) и cos y = 1/4 (откуда
) и cos y = 1/4 (откуда ![]() ). Из всех найденных решений условию
). Из всех найденных решений условию 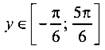 удовлетворяет только значение у = arccos 1/4. Определим
удовлетворяет только значение у = arccos 1/4. Определим ![]() и найдем
и найдем ![]() Таким образом, данная система уравнений имеет единственное решение
Таким образом, данная система уравнений имеет единственное решение ![]()
IV. Задание на уроках и на дом
Решите систему уравнений:

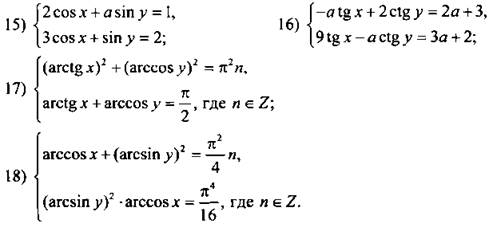
Ответы: ![]()
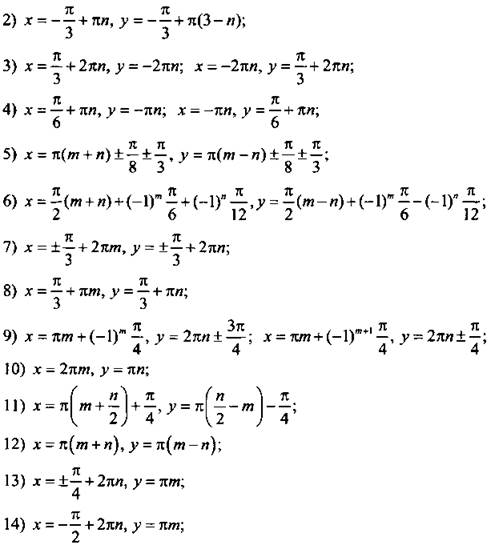
![]() при
при ![]()
![]()
![]() при
при ![]()
![]() t - любое действительное число, кроме
t - любое действительное число, кроме ![]() при
при ![]()
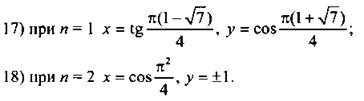
V. Подведение итогов уроков