Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Демонстрационный вариант ГИА (факультативное занятие) - Государственная итоговая аттестация по алгебре (ГИА)
Цели: дать представление о структуре и сложности варианта; разобрать его; отметить его особенности.
Далее приведен вариант экзаменационной работы с решением, по которому можно судить об уровне сложности заданий и их распределении по темам. В части 2 после номера задания в скобках указано число баллов за это задание. Рекомендуем вам самостоятельно выполнить вариант. В случае затруднений можно обратиться к разбору варианта.
Вариант
Часть 1
1. Диаграмма иллюстрирует распределение учащихся школы между начальными, средними и старшими классами. Сколько процентов всех учащихся учится в 10-11 классах этой школы?

2. Найдите сумму, значение которой больше 1.
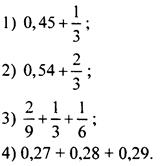
3. На координатной прямой точками изображены числа a и b. Определите, какое из чисел является наибольшим: 2а, 2b или а + b.
![]()
1) а + b;
2) 2 а;
3) 2 b;
4) Для ответа не хватает данных.
4. Найдите значение выражения ![]() при
при ![]()
5. Принтер печатает одну страницу за 6 с. Сколько страниц можно распечатать на этом принтере за t мин?
1) 6t с.;
2) 10t с.;
3) 0,1t c.;
4) t/6 с.
6. Упростите выражение ![]()
7. Найдите значение выражения (27 ∙ 3-4)2.
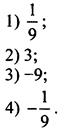
8. Упростите выражение ![]()
9. Решите уравнение ![]()
1) 1;
2) 1,4;
3) 5;
4) 5,4.
10. Какое из уравнений не имеет корней?
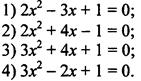
11. Для каждой системы уравнений укажите число ее решений. (Для ответа используйте графики; график уравнения х2 + у2 = 4 изображен на рисунке.)
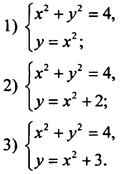
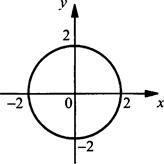
а) нет решений;
б) одно решение;
в) два решения;
г) три решения.
12. Какое из следующих чисел не является решением неравенства 9х – 3 > 10x - 2?
1) -4,9;
2) -1,7;
3) -1,1;
4) -0,7.
13. Сравните, если возможно, числа а и с при условии, что a > b и b ≤ с.
1) a > с;
2) а < с;
3) а ≤ с;
4) сравнить невозможно.
14. В зрительном зале 15 рядов. В первом ряду 10 мест, а в каждом следующем на одно место больше, чем в предыдущем. Сколько мест в зрительном зале?
1) 255;
2) 165;
3) 120;
4) 75.
15. На каком рисунке изображен график функции у = f(х), обладающей свойствами: f(0) = 2 - и функция возрастает на промежутке (-∞; 1]?
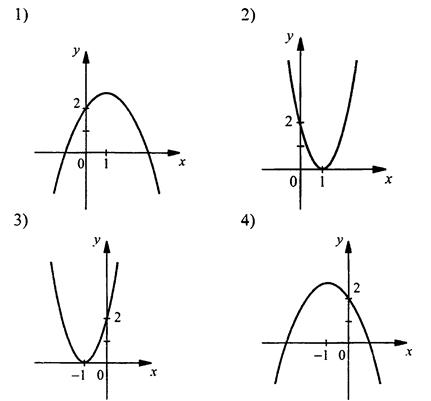
16. График показывает, как менялась цена бензина в течение месяца. Определите, на сколько процентов выросла его цена за месяц.
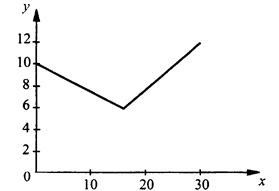
1) на 100%;
2) на 60%;
3) на 20%;
4) на 2%.
17. На 1000 электрических лампочек в среднем приходится 5 бракованных. Какова вероятность купить исправную лампочку?
18. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Часть 2
19 (2). Сократите дробь ![]()
20 (4). Постройте график функции ![]() При каких значениях х функция принимает отрицательные значения?
При каких значениях х функция принимает отрицательные значения?
21 (4). На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине ее можно сделать на 15 мин быстрее, чем на второй?
22 (6). Найдите значение т, при котором точки А(3; 15), В(9; 5) и С(24; m) лежат на одной прямой.
23 (6). При каких значениях к число 0 находится между корнями уравнения х2 - 4х + (2 - k)(2 + k) = 0?