Государственная итоговая аттестация по алгебре (факультативное занятие) - Государственная итоговая аттестация по алгебре (ГИА)

Цель: сообщить основные положения о ГИА и дать рекомендации по написанию экзамена.

Основные положения

В настоящее время возникла и развивается новая форма государственной (итоговой) аттестации по алгебре в 9 классе - аналог Единого государственного экзамена по математике в 11 классе. Такая система уже использовалась при проведении экзамена в 9 классе во многих регионах России: Московской области, Краснодарском крае, Челябинской, Псковской, Новгородской, Кемеровской, Калининградской и других областях.

Основное назначение новой формы экзамена - введение открытой объективной независимой процедуры оценки знаний учащихся. Результаты такой оценки способствуют осознанному выбору дальнейшего пути получения образования, учитываются при формировании профильного 10 класса.

Характеристика экзаменационной работы

Работа состоит из двух частей, каждая из которых направлена на проверку определенных понятий, знаний, навыков, имеет свою систему оценок в баллах и разное оформление на экзамене.

Часть 1 направлена на проверку базовой подготовки учащихся. Проверяются понимание смысла важнейших понятий, знание важнейших фактов, умение применять известные способы решения несложных задач, применять знания в простейших практических ситуациях. Здесь представлены задачи по темам: числа, буквенные выражения, преобразования выражений, уравнения и текстовые задачи, неравенства, функции и графики, последовательности и прогрессии.

В эту часть работы включены 18 заданий с выбором ответа (из четырех приведенных), с кратким ответом и на соотнесение условий задачи и приведенных ответов. В экзаменационный бланк вписывается только ответ, никаких решений не приводится. За каждое верно выполненное задание начисляется 0,5 балла.

Часть 2 направлена на проверку профилированной (повышенного уровня) подготовки учащихся. Проверяются умение решать достаточно сложные задачи с использованием различных фактов и способов, владение исследовательскими навыками, умения найти и применить нестандартные приемы. Здесь представлены задачи по темам: выражения и их преобразования, уравнения и системы уравнений, неравенства, функции, координаты и графики, арифметическая и геометрическая прогрессии, текстовые задачи.

В эту часть работы включены 5 заданий из различных разделов курса. Задания расположены по нарастанию сложности - от относительно простых до достаточно сложных. Предусматривается полная запись хода решения. Каждое задание оценивается (в зависимости от сложности) в 2, 4 и 6 баллов (даны одна задача в 2 балла, две задачи по 4 балла и две задачи по 6 баллов).

На проведение экзамена отводится 240 минут (4 часа). При этом на выполнение части 1 время ограничено - на нее отводится 60 мин.

Экзаменационная работа предлагается в четырех вариантах. Каждому учащемуся в начале экзамена выдается бланк с полным текстом работы. Ответы к заданиям части 1 учащиеся отмечают в бланке с заданиями, вторая часть выполняется на отдельных листах.

Для оценки результатов выполнения работы используются два количественных показателя: рейтинг (сумма баллов за верно выполненные задания) и оценка 2, 3, 4 или 5. Если за часть 1 работы получено менее 3,5 балла, то этот результат не компенсируется выполнением заданий части 2 и ученику ставится оценка 2. Если общий рейтинг по работе выражается дробным числом, то он округляется с избытком до ближайшего целого числа. За часть 1 работы можно максимально получить 9 баллов, за часть 2-22 балла, за всю работу - 31 балл. Соответствие между рейтингом и оценкой: 4-7 баллов - оценка 3,8-15 баллов - оценка 4,16-31 балл - оценка 5.

Общие рекомендации по экзамену

1. Математику надо знать. Чем лучше вы ее знаете, тем больше баллов сможете набрать и претендовать на более высокую отметку в школе и на поступление в профильные классы или школы. Наше пособие позволяет эффективно и успешно подготовиться по всем темам, входящим в экзамен (первые шесть тем).

2. Выполняйте задания экзамена в том порядке, в котором они даны. Задания части 1 существенно проще заданий части 2 и не требуют много времени. Кроме того, к этим заданиям приведены варианты ответов, и можно или определить правильный ответ, или исключить явно неверные ответы (см. далее).

3. При решении заданий части 1 не тратьте время на аккуратность записей и обоснование решений. Ваша задача - определить правильный ответ, который обводится в тексте задания или вписывается на специальном месте.

4. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если после выполнения заданий у вас еще останется время, то вы сможете вернуться к пропущенным заданиям.

5. Контролируйте время на выполнение заданий (на первую часть дается не более 60 мин). Не зацикливайтесь на нерешенной задаче - лучше ее пропустить.

6. В оставшееся время переходите к решению более сложных заданий части 2. Здесь вам понадобятся все умения и навыки, творческий, нестандартный подход к задаче. Даже если вы до конца не решите задачу, то сделанные этапы задания будут оценены. Пугаться этих заданий не следует - они базируются на более простых и известных задачах. Обращайте внимание на обоснованность решений в этих заданиях. Задания части 2 выполняются на отдельных листах.

7. Как правило, в вычислительных задачах ответом является целое число. Если у вас получился другой ответ, быстро проверьте ход решения и математические расчеты.

Советы по проверке заданий части 1 экзамена

В заданиях части 1 надо выбирать правильный ответ из четырех возможных вариантов. Рассмотрим приемы, которые позволяют или определить правильный ответ, или исключить явно неверные ответы. Проиллюстрируем эти приемы примерами из вариантов ГИА.

Способ контрольных точек

Ответ проверяется для нескольких (наиболее простых) значений переменных. Способ применяется в преобразованиях выражений, при решении неравенств и т. д.

Пример 1

Упростите выражение (a - 4)² - 2a(3a - 4).

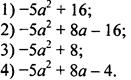
Приведенные ответы отличаются свободным членом. Поэтому подставим, например, значение a = 0 в данное выражение и ответы. При подстановке в выражение получим: (-4)² = 16. При подстановке в ответы только ответ 1 дает тот же результат. Поэтому сразу определяется правильный ответ 1.

Пример 2

Известно, что a - число нечетное. Какое из чисел является четным?

1) 3а;

2) а + 2;

3) 2а + 1;

4) а² + 1.

Возьмем любое нечетное число, например 5, и подставим в ответы. Соответственно, получаем: 15, 7, 11 и 26. Видим, что только для ответа 4 получается четное число.

Пример 3

Сравните a² и а³, если известно, что 0 < a < 1.

1) а² < а³;

2) a² > а³;

3) а²= а³;

4) для сравнения не хватает данных.

Даже не зная свойств числовых неравенств, можно взять любое число а, удовлетворяющее неравенству 0 < а < 1, например число 1/2. Найдем: Так как то а² > а³ и правильный ответ 2.

Способ граничных точек

При решении неравенств (или задач, связанных с неравенствами) ответы могут различаться граничными точками промежутков. Поэтому проверку надо начинать именно с этих точек. Способ похож на предыдущий.

Пример 4

Решите систему неравенств

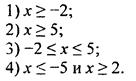
Ответы 1 и 3 отличаются от ответов 2 и 4 тем, что в данную систему входит точка x = -2. Подставим это значение в данную систему и получим: или Так как второе неравенство системы неверно, то ответы 1 и 3 отпадают.

Проверим теперь ответы 2 и 4. Возьмем точку х = -5, входящую в ответ 4, и получим: или Оба неравенства неверны. Поэтому правильный ответ 2.

Пример 5

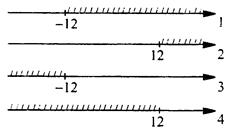
Решите неравенство 2х - 3(х + 4) ≤ х + 12.

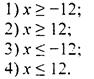
Проверим ответы. Для удобства изобразим ответы на координатных осях. Проверим сначала ответы 3 и 4. Возьмем точку х = -14, входящую только в эти ответы. Получим: 2 ∙ (-14) - 3 ∙ (-14 + 4) ≤ -14 + 12 или 2 ≤ -2. Так как неравенство неверное, то ответы 3 и 4 отпадают. Теперь разберемся с ответами 1 и 2. Возьмем точку а = 0, которая входит только в ответ 1. Получаем: 2 ∙ 0 - 3 ∙ (0 + 4) ≤ 0 + 2 или -12 ≤ 12. Так как неравенство верное, то правильный ответ 1.

Способ оценки величин

В ряде случаев удается оценить величины, входящие в задачу, и выбрать правильный ответ.

Пример 6

Какие целые числа заключены между числами √15 и √35?

1) 16, 17. ..., 34;

2) 3, 4 и 5:

3) 4, 5 и 6;

4) 4 и 5.

Так как 15 ≈ 16, то √15 чуть меньше 4, для оценок будем считать ≈ 3,9. Число 35 ≈ 36, и √35 чуть меньше 6, для оценок будем считать ≈ 5,9. Отметим числа 3,9 и 5,9 на координатной оси. Видно, что в промежуток 3,9 ÷ 5,9 попадают только два целых числа - 4 и 5. Поэтому правильный ответ 4.

Пример 7

Найдите площадь прямоугольника, стороны которого равны √5 + 1 и √5 - 1.

1) 24;

2) 6;

3) 4;

4) 6 - 2√5.

Очевидно, что √5 чуть больше 2 (для оценок √5 ≈ 2,2). Тогда стороны прямоугольника и его площадь примерно равна 3,2 ∙ 1,2 ≈ 3,8. Учитывая, что в ответе 4 величина видим, что наиболее подходящий ответ 3 (который действительно является правильным).

Пример 8

Укажите наименьшее из чисел

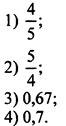
Легко точно или приблизительно записать обыкновенные дроби в виде десятичных: Теперь, сравнив числа 0,8;1,25; 0,67 и 0,7, видим, что наименьшим является число 0,67. Правильный ответ 3.

Способ проверки размерности ответа

В задачах с текстовым содержанием и в задачах, связанных с физикой или геометрией, полезно проверить размерность ответа. Это позволяет сразу отбросить явно неправильные ответы.

Пример 9

Выразите из формулы скорости равноускоренного движения v = v₀ + at время t.

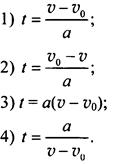
Вспомним размерности величин, входящих в данную формулу. Скорости v и v₀ измеряются в м/с, ускорение a - в м/с² и время t – в с. Проверим размерность правых частей приведенных ответов и получим:

Ответы 3 и 4 сразу отпадают. Варианты 1 и 2 имеют одинаковую размерность, и поэтому приходится использовать здравый смысл. При a > 0 тело ускоряется и v > v₀. Поэтому разность v - v₀ > 0. Тогда в случае 1 получаем: t > 0, в случае 2, наоборот, t < 0. Так как никто не знает, что такое отрицательное время, то правильный ответ 1.

Пример 10

От города до поселка автомобиль доехал за 3 ч. Если бы он увеличил скорость на 25 км/ч, то затратил бы на этот путь на 1 ч меньше. Чему равно расстояние от города до поселка?

Пусть x км - расстояние от города до поселка. Какое уравнение соответствует условию задачи?

В правой части всех уравнений стоит величина увеличения скорости, и она измеряется в км/ч. В левой части числа 2 и 3 соответствуют времени движения автомобиля с увеличенной скоростью и реальной скоростью. Эти числа имеют размерность ч. Определим размерность левых частей приведенных уравнений: 1) км : ч = км/ч; 2) км : ч = км/ч; 3) ч : км = ч/км; 4) ч : км = ч/км. По несоответствию размерностей левой и правой частей уравнения ответы 3 и 4 отпадают. Разберемся с ответами 1 и 2. Так как х – положительная величина, то Потому выражение а выражение Так как в правой части уравнений стоит положительное число 25, то правильный ответ 1.

Способ проверки ответов по условию

Иногда, используя условие задачи, можно сразу проверить ответ.

Пример 11

Решите уравнение

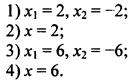
Так как в данном квадратном уравнении нет линейного члена, то его корни являются симметричными числами, т. е. если уравнение имеет корень х₀, то число -х₀ также корень этого уравнения. Поэтому ответы 2 и 4 (которые содержат только один корень) явно не подходят. Проверим ответ 1. Подставим в уравнение, например, значение х = 2 и получим: Поэтому ответ 1 также не подходит. Итак, правильный ответ 3.

Пример 12

Решите уравнение

1) -23;

2) -20;

3) -6;

4) -9.

Проверим приведенные ответы, подставляя их в левую часть уравнения. Получим:

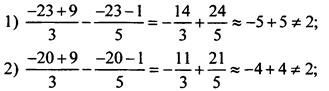
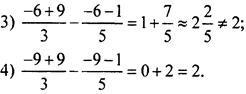Правильный ответ.

Способ обратной задачи

Достаточно часто в задачах, связанных с преобразованиями выражений, проще решить обратную задачу и тем самым проверить приведенные ответы.

Пример 13

Укажите выражение, тождественно равное многочлену 4х² - 6ху.

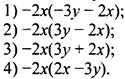
Ответы представляют собой разложение некоторого многочлена на множители. Если при раскрытии скобок получится данный многочлен, то разложение на множители сделано правильно. Так как в данном многочлене коэффициенты членов противоположны по знаку, то в ответах в скобках коэффициенты слагаемых также будут противоположны по знаку. Поэтому ответы 1 и 3 сразу можно отбросить. Раскроем скобки в ответах 2 и 4 и получим:

(данный многочлен);

Итак, правильный ответ 2.

Пример 14

Известно, что верно неравенство х > у - z. Какое из неравенств также является верным?

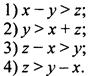
Запишем неравенства в ответах в виде, аналогичном виду данного неравенства: слева - переменная х, справа - переменные у и z. Получаем: Видно, что только в случае 4 неравенство в ответе и данное неравенство совпадают. Поэтому неравенство 4 является верным.

Другие способы

В простейших случаях можно использовать соображения, основанные на обычном здравом смысле и очень поверхностном знании математики.

Пример 15

Средний вес девочек того же возраста, что и Маша, равен 36 кг. Вес Маши составляет 110% среднего веса. Сколько весит Маша?

1) 32,4 кг;

2) 39,6 кг;

3) 36 кг;

4) 3,6 кг.

Так как вес Маши составляет 110% среднего веса (т. е. несколько больше среднего веса), то она весит больше 36 кг. Из приведенных ответов подходит только ответ 2.

Пример 16

Из полного бака, вместимость которого 100 л, через открытый кран вытекает вода со скоростью 5 л/мин. Количество воды у, остающейся в баке, является функцией времени х, в течение которого вытекает вода. Задайте эту функцию формулой.

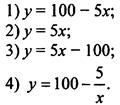
Из здравого смысла понятно, что с течением времени х в баке остается все меньше и меньше воды у. Поэтому у(х) должна быть убывающей функцией. Из приведенных функций только функция 1 у = 100 - 5x является убывающей. Если вам трудно установить монотонность функции, то достаточно сравнить значения приведенных функций, например, при х = 1 и х = 20.

Из приведенных примеров видно, что простые приемы позволяют найти правильные ответы многих заданий, фактически не решая их.