Функции и графики - Итоговое повторение

Цель: вспомнить графики основных функций.

Ход уроков

I. Сообщение темы и цели уроков

II. Контроль усвоения материала (самостоятельная работа)

Вариант 1

Упростите выражение:

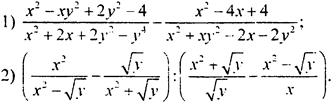
Вычислите:

Вариант 2

Упростите выражение:

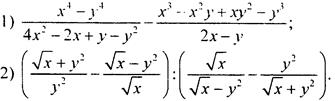
Вычислите:

III. Повторение пройденного материала

Функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу (закону) число у из множества Е, зависящее от х. Такое правило (закон) является функцией у = f(x) с областью определения D и областью значений Е.

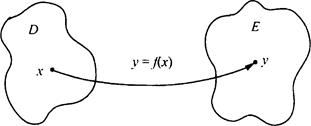
При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).

Точка пересечения графика функции с осью ординат равна значению функции у = f(x) при х = 0, т. е. у = f(0). Точки пересечения графика функции с осью абсцисс (их еще называют нулями функции) являются корнями уравнения f(x) = 0.

Промежутки знакопостоянства функции - те значения переменной х, при которых функция принимает положительные (у > 0) и отрицательные (у < 0) значения.

Монотонность - возрастание или убывание функции. Функция у = f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции (т. е. если х₂ > х₁, то f(x₂) > f(х₁)). Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если х₂ > х₁, то f(x₂) < f(х₁)).

Область определения функции называется симметричной, если в нее входит и точка x₀, и точка (-х₀) (т. е. точка, симметричная точке х₀ относительно начала числовой оси).

Функция называется четной, если при изменении знака аргумента значение функции не меняется, т. е. f(-x) = f(x). График четной функции симметричен относительно оси ординат. Функция называется нечетной, если при изменении знака аргумента значение функции также меняется на противоположное, т. e. f(-x) = -f(x). График нечетной функции симметричен относительно начала координат.

Основные виды рациональных функций

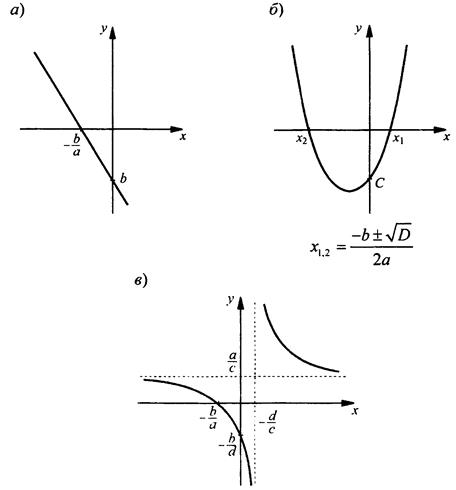
а) Линейная функция у = ax + b (где а и b - некоторые числа). График функции - прямая линия.

б) Квадратичная функция у = ах² + bх + с (где а, b, с - некоторые числа). График функции - парабола.

в) Дробно-линейная функция (где а, b, c, d - некоторые числа). График функции - гипербола.

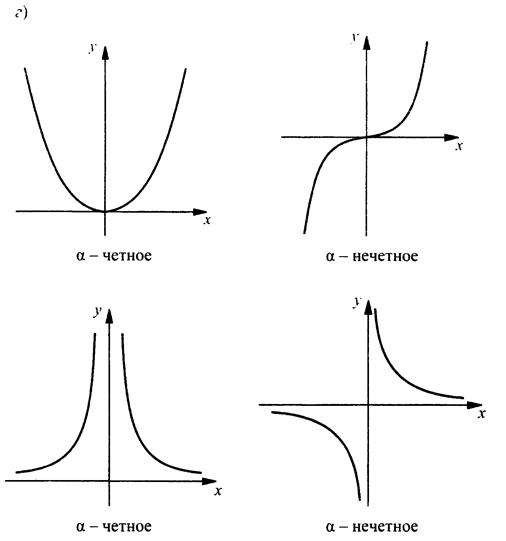
г) Степенная функция у = х^а (пока будем рассматривать целые значения а (а ≠ 0, а ≠ 1)).

Для некоторых значений чисел a, b, с, d, а приведем графики этих функций.

IV. Задание на уроках

№ 1, 5, 10, 15, 17, 19, 23, 25, 29, 33, 37, 42, 45, 50, 53, 61, 67, 72, 79, 84, 87, 90, 92, 94, 97, 102, 106, 116, 122, 131, 138, 143, 147, 160, 167, 174, 181.

V. Задание на дом

№ 2, 6, 14, 16, 18, 20, 24, 26, 30, 34, 38, 43, 46, 51, 55, 63, 68, 73, 80, 85, 88, 91, 93, 95, 103, 107, 117, 123, 133, 139, 148, 161, 168, 175, 182.

VI. Подведение итогов уроков