Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Функции у = х-n (n ∈ N), их свойства и графики - Числовые функции
Цель: рассмотреть свойства и график функции у = х-n (n ∈ N).
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Дана функция f(х) = 2(х - 1)4. Вычислите 2f(0) – 3f(1) + 4f(2).
2. Сравните числа: а) (-7,2)6 и (6,1)6; б) (-4,8)3 и 2,73.
3. Постройте график функции у = (х + 1)4 - 2.
Вариант 2
1. Дана функция f(х) = -2(х + 1)4. Вычислите 6f(-1) + 4f(0) – 3f(1).
2. Сравните числа: а) (-9,3)4 и (7,3)4; б) (-7,8)5 и 4,75.
3. Постройте график функции у = (х + 1)3 - 2.
III. Изучение нового материала
Рассмотрим теперь функции у = х-n (n ∈ N). Такие функции называют степенными функциями с отрицательным целыми показателями. По определению степени с отрицательным показателем рассматриваемые функции можно записывать и в виде y = 1/xn. При n = 1 функция у = 1/x была изучена. Ее графиком является гипербола. Также необходимо обсудить свойства и график степенной функции при любом натуральном n. Эти характеристики существенно различаются в зависимости от четности или нечетности числа n.
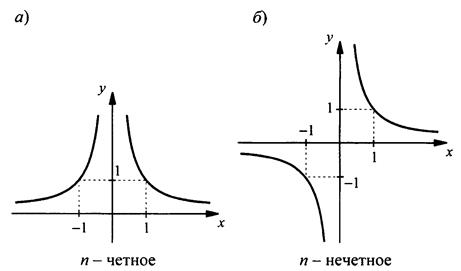
Приведем свойства функции у = х-n при четном n.
1) Область определения функции - все значения х, кроме нуля, т.е. D(f) = (-∞; 0)U(0; +∞).
2) График не пересекает осей координат. При этом ось абсцисс является горизонтальной асимптотой графика функции, ось ординат - вертикальной асимптотой графика (напомним, что асимптотой графика функции называют прямую, к которой при определенных условиях неограниченно близко приближается график).
3) При всех х из области определения y > 0. Поэтому график расположен в первой и второй координатных четвертях.
4) Функция четная: у(-х) = у(х). Следовательно, график функции симметричен относительно оси ординат.
5) Функция возрастает в промежутке (-∞; 0) и убывает в промежутке (0; +∞). Наименьшего и наибольшего значений функция не имеет.
6) Функция ограничена снизу: у > 0.
7) Область значений функции E(f) = (0; +∞).
8) График функции представлен на рис. а.
Рассмотрим также свойства функции у = х-n при нечетном n (они аналогичны свойствам функции у = 1/x).
1) Область определения функции - все значения х, кроме нуля, т.е. D(f) = (-∞; 0)U(0; +∞)).
2) График не пересекает осей координат. При этом ось абсцисс является горизонтальной асимптотой графика функции, ось ординат - вертикальной асимптотой.
3) При х > 0 значения у > 0, при х < 0 - у < 0. Поэтому график расположен в первой и третьей координатных четвертях.
4) Функция нечетная: y(-x) = -у(х). Следовательно, график функции симметричен относительно начала координат.
5) Функция убывает в области определения. Наименьшего и наибольшего значений функция не имеет.
6) Функция не ограничена.
7) Область значений функции E(f) ∈ (-∞; 0)U(0; +∞).
8) График функции представлен на рис. б.
Пример 1
Сравним числа 0,17-3 и 0,19-3.
Сравниваются два значения степенной функции у = х-3 при х = 0,17 и х = 0,19. При n = 3 функция убывающая. Поэтому 0,17-3 > 0,19-3.
Пример 2
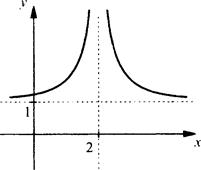
Построим график функции ![]()
Такой график получается параллельным переносом графика у = 1/x2 на две единицы вправо и на одну единицу вверх. Поэтому график имеет вертикальную асимптоту х = 2 и горизонтальную асимптоту у = 1. При этом график симметричен относительно прямой х = 2.
Пример 3
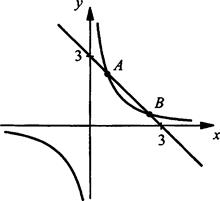
Определим число решений системы уравнений 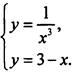
Построим графики функций y = 1/x3 и у = 3 - х. Видно, что графики функций пересекаются в двух точках: А и В. Поэтому данная система уравнений имеет два решения.
Пример 4
Даны функции f(x) = х-3 и g(x) = х4. Докажем, что выполняется равенство (f(х2))2=(g(x))-3.
Сначала найдем f(x2) = (х2)-3 = х-6 и (f(х2))2 = (х-6)2 = х-12. Также найдем (g(x))-3= (х4)-3 = х-12. Видно, что данное равенство действительно выполняется.
IV. Контрольные вопросы
1. Перечислите основные свойства и приведите график функции у = х-n для четных n.
2. Приведите свойства и график степенной функции у = х-n для нечетных n.
V. Задание на уроках
§ 13, № 2 (а, б); 4 (а, в); 5; 7; 11 (б); 12; 19; 21 (а); 22 (а, б); 24.
VI. Задание на дом
§ 13, № 2 (в, г); 4 (б, г); 6; 8; 11 (г); 13; 20; 21 (б); 22 (в, г); 25.
VII. Подведение итогов уроков