Функция у = xⁿ (n ∈ N), ее свойства и графики - Числовые функции

Цель: рассмотреть свойства и график функции у = xⁿ (n ∈ N).

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Постройте график функции:

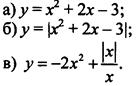
2. Парабола у = ax² + bх + с проходит через точки А(-1; 0), 5(0; 3) и С(2; -3). Найдите коэффициенты а, b, с.

Вариант 2

1. Постройте график функции:

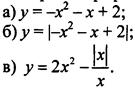
2. Парабола у = ах² + bх + с проходит через точки А(-1; 4), B(0; 1) и С(2; 7). Найдите коэффициенты a, b, с.

III. Изучение нового материала

Функцию у = хⁿ (где х - независимая переменная, n - натуральное число) называют степенной функцией с натуральным показателем. Частные случаи такой функции для n = 1, 2 (т. е. у = х, у = х²) мы уже рассматривали. Известны свойства и графики этих функций. Теперь необходимо обсудить свойства и график степенной функции при любом натуральном n. Эти характеристики существенно различаются в зависимости от четности или нечетности числа n.

Приведем свойства функции у = хⁿ при четном n (они аналогичны свойствам функции у = x²).

1) Область определения функции - промежуток (-∞; +∞).

2) Если х = 0, то у = 0. Поэтому график функции проходит через начало координат.

3) Если х ≠ 0, то у > 0. Следовательно, график функции расположен в первой и второй координатных четвертях.

4) Функция четная: y(-x) = у(х). Поэтому график функции симметричен относительно оси ординат.

5) Функция возрастает в промежутке [0; +∞) и убывает в промежутке (-∞; 0]. Наименьшее значение у = 0 функция принимает при х = 0, наибольшего значения функция не имеет.

6) Функция ограничена снизу: у ≥ 0.

7) Область значений функции - промежуток [0; +∞).

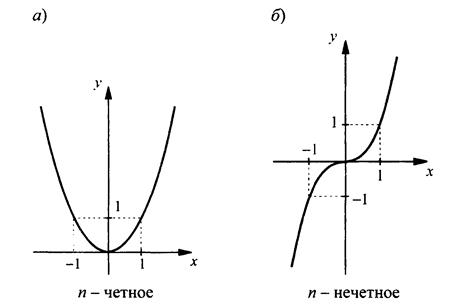
8) График функции представлен на рис. а.

Рассмотрим также свойства функции у = хⁿ при нечетном n (они аналогичны свойствам функции у = х³).

1) Область определения функции - промежуток (-∞; +∞).

2) Если x = 0, то у = 0. Поэтому график функции проходит через начало координат.

3) Если х < 0, то у < 0, и если х > 0, то у > 0. Следовательно, график функции расположен в первой и третьей координатных четвертях.

4) Функция нечетная: y(-х) = -у(х). Поэтому график функции симметричен относительно начала координат.

5) Функция возрастает на всей области определения.

6) Функция не ограничена.

7) Область значений функции - промежуток (-∞; +∞).

8) График функции представлен на рис. 6.

Пример 1

Дана функция f(х) = х³. Вычислим выражение f(3) – 4f(2) + 7f(1).

Чтобы найти значение функции при данном значении аргумента, надо подставить этот аргумент в формулу, задающую функцию, и выполнить действия. Получаем: f(3) – 4f(2) + 7f(1) = 3 - 4 ∙ 2³ + 7 - 1³ = 27 – 4 ∙ 8 + 7 ∙ 1 = 27 - 32 + 7 = 2.

Пример 2

Сравним числа: а) (-3,2)⁴ и (-1,8)⁴; б) 2,4⁴ и 2,7⁴; в) (-6,5)³ и (-4,8)³; г) (-6,5)³ и (-4,8)⁵; д) 2,8³ и 4,1³.

При решении подобных задач учитывают монотонность соответствующей функции, f(x) = х⁴. Эта функция убывает на промежутке (-∞; 0]. Так как -3,2 < -1,8, то f(-3,2) > f(-1,8) или (-3,2)⁴ > (-1,8)⁴. На промежутке [0; +∞) эта функция возрастает. Так как 2,4 < 2,7, то и f(2,4) < f(2,7) или 2,4⁴ < 2,7⁴.

Теперь рассмотрим функцию g(x) = х³. Такая функция возрастает на всей области определения. Так как -6,5 < -4,8 и 2,8 < 4,1, то и g(-6,5) < g(-4,8) и g(2,8) < g(4,1) или (-6,5)³ < (-4,8)³ и 2,8³ < 4³.

Пример 3

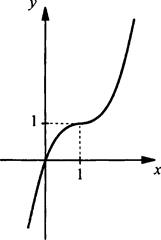
Построим график функции у = (х - 1)³ + 1.

Учтем ранее изученные способы преобразования графиков. График функции у = (х - 1)³ + 1 получается сдвигом графика функции у = х³ на одну единицу вправо и на одну единицу вверх.

Пример 4

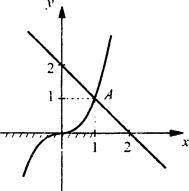
Решим неравенство х³ ≤ 2 - х.

Решим данное неравенство графически. Построим графики функций у = х³ и у = 2 - х. Эти графики пересекаются в единственной точке A(1; 1). По условию задачи надо найти те значения х, при которых первый график расположен не выше второго графика. Из рисунка видно, что условие задачи выполняется на промежутке (-∞; 1].

IV. Контрольные вопросы

1. Перечислите основные свойства и приведите график функции у – хⁿ для четных n.

2. Приведите свойства и график степенной функции для нечетных п.

V. Задание на уроках

§ 12, № 1 (а, г); 2; 5 (б); 13 (а, в); 15 (а); 17 (а, б); 18 (в, г); 20 (а); 22; 24 (а, б); 25 (в, г); 27; 29; 32 (а); 33 (а, г); 34.

VI. Задание на дом

§ 12, № 1 (б, в); 3; 5 (в); 13 (б, г); 15 (г); 17 (в, г); 18 (а, б); 20 (г); 23; 24 (в, г); 25 (а, б); 28; 30; 32 (б); 33 (б); 35.

VII. Подведение итогов уроков