Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМЕ ЧЕТЫРЕХУГОЛЬНИКИ, МНОГОУГОЛЬНИКИ - Урок 2 - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цель деятельности учителя |
Создать условия для систематизации знаний по теме “Четырехугольники и многоугольники”, повторения основных определений, свойств, признаков четырехугольников и многоугольников, для подготовки к сдаче ГИА |
|||
|
Термины и понятия |
Параллелограмм и его свойства; признаки параллелограмма; прямоугольник, ромб, квадрат и их свойства; трапеция, многоугольник, правильные многоугольники |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для фронтальной работы, индивидуальной работы, домашней работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Систематизировать теоретические знания |
(Ф/И) 1. Проверить выполнение домашнего задания. 2. Организовать выполнение самостоятельной работы (15 мин). Задания взяты из тестов ГИА.
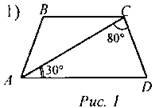
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
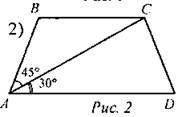
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. 3) Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах. 4) Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах. 5) Углы выпуклого четырехугольника относятся как 1 : 2 : 3 : 4. Найдите меньший угол. Ответ дайте в градусах |
Решение: 1) Так как в треугольнике сумма всех углов равна 180°, то угол ADC равен 180° - 30° - 80° = 70°. В равнобедренной трапеции углы BCD и CDA - односторонние, значит, угол АВС равен 110°. Ответ: 110. 2) Так как больший угол равнобедренной трапеции - угол АВС или угол BCD, то сведем задачу к нахождению угла BCD. В равнобедренной трапеции противолежащие углы - смежные, значит, угол BCD равен 180° - 45° - 30° = 105°. Ответ: 105. 3) У параллелограмма противоположные углы равны, значит углы, прилежащие к одной стороне, являются меньшим и большим углами параллелограмма. Обозначим меньший угол за х, тогда больший угол за х + 40°. Так как у параллелограмма суммы соседних углов, то есть углов, прилежащих к одной стороне, равны 180°, то получим х + х + 40° = 180°; 2х = 140°; х = 70°. Таким образом, наименьший угол параллелограмма равен 70°. Ответ: 70°. 4) Пусть х - меньший угол параллелограмма, а 2х - больший угол. У параллелограмма противоположные углы равны, таким образом имеем уравнение: 6х = 360°; х = 60°. Таким образом, меньший угол параллелограмма равен 60°. Ответ: 60°. 5) Пусть х - меньший угол четырехугольника. Так как сумма углов выпуклого четырехугольника равна 360°, имеем уравнение: х + 2х + 3х + 4х = 360°; 10х = 360° = 36°. Таким образом, меньший угол равен 36°. Ответ: 36 |
||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Совершенствовать навыки решения задач |
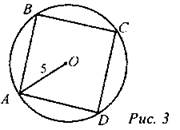
(Ф/И) 1. Вспомнить формулы для вычисления площадей, радиуса описанной около правильного “-угольника окружности. 2. Решить задачи по готовым чертежам: 1) Дано: ABCD - правильный. Найти: AD, r.
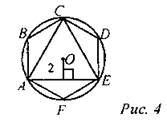
2) Дано: ABCDEF - правильный. Найти: АВ и АС.
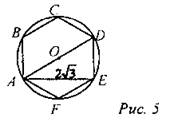
3) Дано: ABCDEF - правильный. Найти: SABCDEF, R.
3. Решить текстовые задачи. Задачи:
1) На рисунке 6 AEFC - прямоугольник; АС = 10 см, АЕ = 3 см, ВМ = AM. а) Докажите, что MN - средняя линия треугольника АВС. б) Найдите AAMNC. в) Найдите SABC. 2) В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке Е; АВ = a; AD = b. Найдите: а) отрезки BE и ЕС; б) отрезки ВК и KD и SABE, если К - точка пересечения АЕ и BD, а угол А равен 60°. 3) На рисунке 7 ABCD - параллелограмм, угол 1 равен углу 2. а) Докажите, что четырехугольник BFDK - параллелограмм, и найдите его площадь и периметр, если KF = 10 см, BD = 6 см, ∠KOD = 150°. б) Каким условиям должны удовлетворять отрезки KF и BD, чтобы параллелограмм BFDK был прямоугольником (ромбом, квадратом)? 4) Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см. Найдите: а) стороны и высоту параллелограмма, проведенную из вершины тупого угла; б) диагонали параллелограмма; в) площадь параллелограмма. 5) В параллелограмме ABCD (рис. 8) проведена биссектриса АK угла А, точка К делит сторону ВС на отрезки ВК = 4 см и КС = 2√2 см. Расстояние между параллельными прямыми AD и ВС равно 2√2 см. Найдите: а) углы параллелограмма; б) площадь треугольника АВС; в) радиус окружности, описанной около треугольника DKC |
|||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Перечислите все формулы для нахождения площадей четырехугольников. - Задайте три вопроса по теме урока. - Составьте синквейн к уроку |
(И) Домашнее задание: повторить теорию метода координат; решить задачи: 1. Около правильного треугольника описана окружность, и в него вписана окружность. Радиус большей окружности равен 4√3 см. Найдите радиус меньшей окружности. 2. Периметр правильного четырехугольника, вписанного в окружность, на 16(√2 - 1) см меньше периметра правильного четырехугольника, описанного около этой же окружности. Найдите радиус окружности |
|||