ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА

Цель деятельности учителя

Создать условия для повторения формулы суммы углов выпуклого многоугольника, свойств биссектрисы угла и серединного перпендикуляра к отрезку, теорем вписанной и описанной около треугольника окружностях, признака равнобедренного треугольника, свойств касательной к окружности, для введения понятия правильного многоугольника, выведения формулы для вычисления угла правильного “-угольника и ее применения

Термины и понятия

Выпуклый многоугольник, правильный многоугольник, равнобедренный треугольник, касательная, описанная и вписанная окружности, серединный перпендикуляр

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют формулировать определение правильного многоугольника, находить углы

Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют работать в группе.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные ресурсы

• Задания для фронтальной работы, групповой работы

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Повторить ранее изученный материал

(Ф)

1. Сообщить результаты контрольной работы и проанализировать допущенные ошибки.

2. Повторить формулу суммы углов выпуклого многоугольника и записать ее.

3. Сформулировать свойство биссектрисы угла и признак равнобедренного треугольника.

4. Повторить теорему об окружности, описанной около треугольника.

5. Устно решить задачи:

1) Сколько сторон имеет n-угольник, если сумма его внутренних углов равна: а) 1260°; б) 1980°?

2) Назовите выпуклый четырехугольник, у которого все внешние углы прямые.

3) Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов равна сумме внешних?

4) Сколько сторон имеет выпуклый многоугольник, если все его внешние углы тупые?

6. Решить задачи на доске и в тетрадях:

1) Все углы выпуклого пятиугольника равны друг другу. Найдите величину каждого угла.

2) Докажите, что треугольник, две высоты которого равны, является равнобедренным.

3) Четырехугольник ABCD вписан в окружность. Докажите, что ∠А + ∠C = ∠В + ∠D

II этап. Мотивация к деятельности

Цель деятельности

Совместная деятельность

Решение задач с целью подготовки учащихся к восприятию новой темы

(Г)

Класс делится на группы. Каждой группе предлагается решить задачи:

1) BE - биссектриса угла АВС, точка Е удалена от стороны ВС на расстояние 5 см. Найдите расстояние от точки Е до стороны АВ.

2) В ∆АВС серединный перпендикуляр MN к стороне АС равен ее половине. Докажите, что АВ > МС.

3) Вычислите радиусы вписанной и описанной около треугольника окружностей, если известно, что стороны треугольника 5, 6 и 7 см.

Затем учащиеся представляют свои решения, идет обсуждение и одновременное повторение теории

III этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Ввести понятие правильного многоугольника

(Ф)

1. Ввести понятие правильного многоугольника.

2. Выполнить задания:

1) Какие правильные многоугольники уже рассматривались нами в курсе геометрии?

2) Приведите примеры такого выпуклого многоугольника, у которого:

а) все стороны равны, но он не является правильным (ромб с острым углом);

б) все углы равны, но он не является правильным (прямоугольник с неравными сторонами).

3. Предложить учащимся вывести формулу для вычисления угла правильного многоугольника в группах. Для этого необходимо решить задачу: чему равен каждый из углов правильного а) десятиугольника; б) n-угольника?

4. Решить задачи № 1081 (в) и 1083 (в) на доске и в тетрадях.

5. Сформулировать и доказать теорему об окружности, описанной около правильного многоугольника (с. 271, рис. 307)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

На простейших задачах отработать применение изученной формулы

(Ф/И)

1. Решить задачи № 1086 и 1084 (б, д).

2. Обсудить решения задач № 1080 и 1082 (устно)

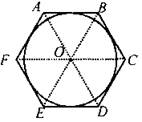
№ 1086.

Дано: ABCDEF - правильный 6-угольник.

Доказать: биссектрисы углов пересекаются или совпадают.

Доказательство:

1) Так как ∠A = ∠B = ∠C = ∠D = ∠E = ∠F (по определению), то

2) Так как биссектрисы пересекаются в центре окружности, вписанной в 6-угольник, то ∠COD = 60°, ∠COE = 120°, ∠COF = 180°, то есть биссектрисы или пересекаются или лежат на одной прямой (диаметр описанной окружности). Это справедливо для любого правильного многоугольника.

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что сегодня повторили на уроке?

- Какой многоугольник называется правильным?

- По какой формуле можно найти угол правильного многоугольника?

(И) Домашнее задание: изучить материалы пунктов 109-110; ответить на вопросы 1-3, с. 284; решить задачи № 1081 (а, д), 1083 (г), 1084 (а, в), 1129