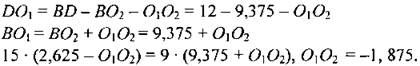Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ОКРУЖНОСТЬ» - Урок 2 - ОКРУЖНОСТЬ
|
Цель деятельности учителя |
Создать условия для систематизации теоретического материала главы, подготовки к контрольной работе; совершенствовать навыки решения задач по теме “Окружность” |
|||
|
Термины и понятия |
Описанная окружность, вписанная окружность, описанный четырехугольник, вписанный четырехугольник, вписанные углы, центральные углы, дуги |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять изученные понятия и методы для решения задач |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|||
|
Образовательные ресурсы |
• Учебник. • Задания для групповой работы |
|||
|
I этап. Решение задач |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Способствовать подготовке к контрольной работе путем решения задач разного уровня сложности |
1. Собрать домашние самостоятельные работы. (Г) 2. Каждой группе даются одинаковые задачи. Учащиеся решают их, затем проводится обсуждение и презентация решений. Задача 1. Через точку А окружности проведены диаметр АС и две хорды АВ и AD так, что хорда АВ равна радиусу окружности, точка D делит полуокружность АС на две равные дуги. Найдите углы четырехугольника ABCD, если точки С и D лежат по разные стороны от диаметра АС. Решение:
1) ∠ABC = ∠ADC = 90°, как вписанные углы, опирающиеся на диаметр. 2) ∆АОВ - равносторонний, так как АО = ВО как радиусы, а хорда АВ равна радиусу, тогда ∠BAO = 60°, ∠BCO = 30°. 3) Точка D делит полуокружность АС на две равные дуги AD и DC, поэтому хорды AD и DC равны, то есть ∆ADC - равнобедренный прямоугольный, поэтому ∠DAC =∠DCA = 45°. 4) ∠BAD = ∠BAC + ∠DAC = 60° + 45° = 105°. 5) ∠BCD = ∠BCO + ∠DCA = 30° + 45° = 75°. Задача 2. Основание равнобедренного треугольника равно 18 см, а высота, проведенная к нему, равна 12 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Решение:
∆AO2D - прямоугольный, по теореме Пифагора АО22 = AD2 + DO22. Точка O2 - центр описанной окружности - лежит на биссектрисе, медиане, высоте, а значит, на серединном перпендикуляре, проведенном к основанию.
Центр вписанной окружности также лежит на BD. АО1 - биссектриса ∠BAC, следовательно АВ : ВО1 = AD : DO1. По теореме Пифагора в ∆ABD: АВ2 = AD2 + BD2 = 81 + 144 = 225, значит, АВ = 15 см. Так как ВO2 = R, то:
Так как O1O2 < 0 => О1 лежит между точками В и O2, тогда DO1 - O1O2 = 2,625 + 1,875 = 4,5 см |
|||
|
II этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И). - Проанализируйте свою работу в группе, выражая это словами: “помощь”, “вместе”, “совет”, “один”, “помогли”, “все”, “посоветовал”, “рассказывал”, “подружились”, “друг” и т. п. |
(И) Домашнее задание: решить № 732, 725, 726; подготовиться к контрольной работе |
|||