Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ. РЕШЕНИЕ ЗАДАЧ - ОКРУЖНОСТЬ
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач по теме |
|||
|
Термины и понятия |
Окружность, хорда, радиус, диаметр, касательная |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
|||
|
I этап. Проверка домашнего задания |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень усвоения теоретического материала |
(Ф) 1. Привести доказательство признака касательной к окружности. (Заслушать одного ученика.) 2. Проверить выполнение домашнего задания и ответить на вопросы учащихся |
|||
|
II этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Совершенствовать навыки решения задач по теме |
(И) Учащиеся решают самостоятельную работу на листочках и сдают учителю на проверку. Вариант I 1. КМ и KN - отрезки касательных, проведенных из точки К к окружности с центром О. Найдите KM и KN, если ОК = 12 см, ∠MON = 120°. 2. Диагонали ромба ABCD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС. Вариант II 1. Найдите отрезки касательных АВ и АС, проведенных из точки А к окружности радиуса r, если r = 9 см, ∠BAC = 120°. 2. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD |
|||
|
III этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач по теме |
(Ф/И) 1. Решение задач по готовым чертежам.
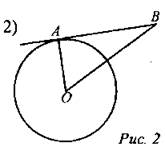
Дано: R = 5, АВ - касательная. Найти: ОВ.
Дано: АВ - касательная; АВ = 12, OB = 13. Найти: R окружности.
Дано: АВ, ВС - касательные, ОВ = 2, АО = 4. Найти: ∠BOC.
Дано: АВ - касательная, R = 6, АО = ОВ. Найти: АО.
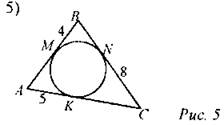
Дано: М, N, К - точки касания. Найти: РABC.
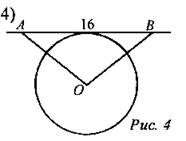
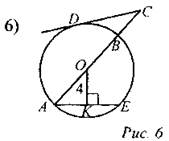
Дано: АВ = 10 см, О – центр окружности, CD – касательная, АЕ || CD. Найти: ОС. 2. Решение задач из учебника (№ 647) |
Ответы: 1) OB = 5√2. 2) R = 5. 3) ∠BOC = 120°. 4) AО = 10. 5) РАВС = 34. 6) ОС = 6,25. № 647.
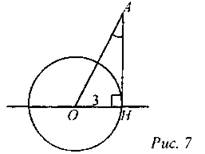
Дано: окружность (О; 3 см). Найти: является ли АН касательной? а) Если ОА = 5 см, АН = 4 см. Рассмотрим ∆AНО: ОА = 5, АН = 4, ОН = 3. 52 = 42 + 32; 25 = 25, значит, ∆AHO - прямоугольный, ∠OHA = 90°, следовательно, АН - касательная. б) Если ∠HAO = 45°, ОА = 4 см. Рассмотрим ∆АНО: ОН = 3, ОА = 4, ∠HAO = 45°. Если предположить, что ∠H = 90°, то АН = ОН = 3, следовательно, АО = 3√2, что противоречит условию АО = 4, значит, предположение неверно, тогда АН не является касательной. в) Если ∠HAO = 30°, ОА = 6 см. Рассмотрим ∆АНО: ОА = 6, ОН = 3, ∠A =30°. Так как ОН = 1/2ОА, следовательно, ∠H= 90°, а значит АН - касательная окружности |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф) - Что сегодня повторили на уроке? - Какие задачи вызвали у вас затруднения? Почему? |
(И) Домашнее задание: № 648; решить задачу (по желанию): Две окружности разных диаметров внешне касаются. К ним проведены две общие касательные АС и BD, где А и В - точки касания с первой окружностью, а С и D - со второй. Докажите, что ACDB - равнобокая трапеция |
|||