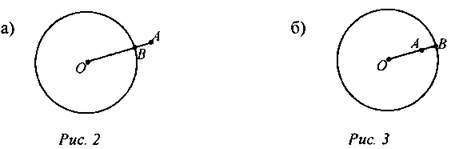Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ - ОКРУЖНОСТЬ
|
Цель деятельности учителя |
Создать условия для рассмотрения различных случаев взаимного расположения прямой и окружности |
|
|
Термины и понятия |
Окружность, хорда, радиус, диаметр, касательная |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной, групповой работы |
|
|
I этап. Актуализация знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Подвести итог контрольной работы, решить задачи, подготавливающие к изучению новой темы |
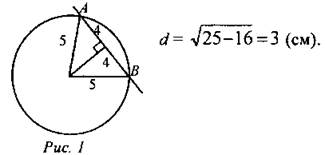
(Ф) 1. Анализ контрольной работы. 2. Решение задач (устно). Вспомнить, что такое окружность, ее элементы. 1. Радиус окружности 5 см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.
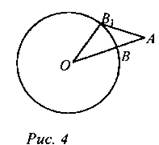
2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если: а) ОА = 12 см, r = 8 см; б) АО = 6 см, r = 8 см. б) АО = 6 см, r = 8 см.
АВ = ОА - r, АВ = 12 - 8 = 4 (см) АВ = r - ОА; АВ = 8 - 6 = 2 (см) 3. Докажите, что АВ < АВ1, используя неравенство треугольника. Имеем ОА < ОВ1 + АВ1, ОВ + АВ < ОВ1 + АВ1, так как ОВ = ОВ1 = r, то АВ < АВ.
|
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выяснить, от чего зависит взаимное расположение прямой и окружности |
(Ф/Г/И) Задача. Даны окружность радиуса г и прямая р, не проходящая через центр О окружности. Расстояние от точки О до прямой р равно d. Сколько точек пересечения могут иметь данные окружность и прямая, если: a) d < r, б) d = r; в) d > r? Для решения данной задачи класс можно разбить на творческие группы по 3-4 ученика в каждой, у каждой группы - свое задание (рассмотреть один из случаев по указанию учителя). Проводится обсуждение решения задачи. В ходе обсуждения на доске необходимо выполнить рис. 211 (а, б, в) из учебника на с. 163 и записать краткое решение задачи |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
На простых задачах отработать взаимное расположение прямой и окружности |
(Ф) Решить № 631 (а, г, д) (устно), 632 |
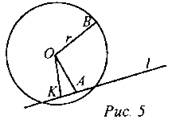
№ 632.
Дано: окружность (О; r), OA = d, OB = r, d < r, А є l. Доказать: l - секущая. Доказательство: 1) Если l ⊥ ОА, то d < r и по определению l - секущая. 2) Если l не ⊥ ОА, то OK ⊥ l и прямоугольный ОА - гипотенуза, значит ОА > ОК. Так как по условию r > ОА, r > ОК, значит l - секущая по определению |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Что нового узнали на уроке? - Каково взаимное расположение прямой и окружности? - Составьте синквейн к уроку |
(И) Домашнее задание: вопросы 1,2, с. 184; № 631 (б, в), 633; выполнить работу над ошибками, допущенными в контрольной работе |
||