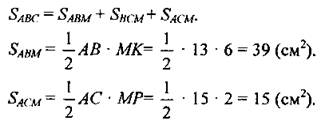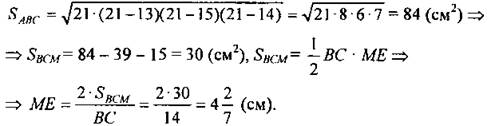РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА. ФОРМУЛА ГЕРОНА - Урок 2 - ПЛОЩАДЬ

Цель деятельности учителя

Создать условия для совершенствования навыков решения задач по теме “Площадь”, используя теорему Пифагора, формулу Герона

Термины и понятия

Прямоугольный треугольник, катеты, гипотенуза, формула Герона

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять изученные понятия, методы для решения задач

Познавательные: осуществляют логические действия; формулируют ответы на вопросы.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.

Коммуникативные: умеют разрешать конфликты на основе согласования позиций и учета интересов.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы______

• Учебник.

• Задания для фронтальной и индивидуальной работы

I этап. Актуализация опорных знаний

Проверка домашнего задания

Цель деятельности

Совместная деятельность

Проверить степень усвоения теоретического материала и умения его применять при решении задач

(Ф)

1. Ответить на вопросы учащихся по выполнению домашнего задания.

2. Провести математический диктант:

1) Записать формулу для вычисления площади треугольника.

2) Записать формулу для вычисления площади прямоугольного треугольника.

3) Записать формулу для вычисления площади равностороннего треугольника.

4) Записать формулу для вычисления площади прямоугольника.

5) Записать формулу для вычисления площади параллелограмма.

6) Записать формулу для вычисления площади ромба.

7) Записать формулу для вычисления площади трапеции.

8) Записать формулу Герона

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Закрепить умение применять формулы площадей многоугольников и теорему Пифагора при решении задач

(Ф) 1. На доске и в тетрадях решить задачи № 504, 517. К доске вызываются два ученика, один из них решает самостоятельно задачу № 504, другой - № 517. На местах учащиеся решают обе задачи, а затем проверяют решение с доски, ищут ошибки в своем решении и в решении на доске, высказывают свое мнение о правильности решения задач.

2. Решить задачу № 525 самостоятельно

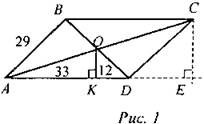
№ 504.

Решение:

Проведем высоту параллелограмма СЕ. Так как OK ⊥ AD и СЕ ⊥ AD, О - середина АС, то по теореме Фалеса АК = КЕ = 33 см, тогда DE = КЕ - KD = 21 см. В ∠DCE ∠E = 90°. DC =29 см. DE = 21 см. тогда по теореме Пифагора СЕ² = CD² - DE² = 841 - 441 = 400 => СЕ = 20 см.

S_ABCD = AD ∙ СЕ = (33 + 12) ∙ 20 = 900 (см²).

Ответ: 900 см².

№ 517.

1-й способ.

S_ABCD = S_ABC + S_ACD. ∆АВС и ∆ACD - прямоугольные по теореме, обратной теореме Пифагора, так как 5² + 12² = 13², 9² + 12² = 15². Площадь прямоугольного треугольника вычисляется по формуле S = ab/2, где а и b - катеты треугольника.

2-й способ.

По формуле Герона где а, b, с - стороны треугольника.

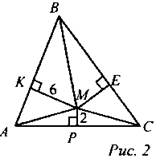
Ответ: 84 см².

№ 525.

По формуле Герона где

Ответ:

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие трудности возникли у вас при решении задач?

- Оцените свою работу на уроке

(И) Домашняя работа: решить № 503, 518, подготовиться к контрольной работе