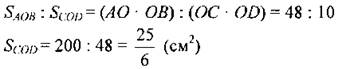ПЛОЩАДЬ ТРЕУГОЛЬНИКА - Урок 2 - ПЛОЩАДЬ

Цель деятельности учителя

Создать условия для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу

Термины и понятия

Площадь треугольника, равновеликие фигуры, отношение площадей

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом

Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.

Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи.

Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной и фронтальной работы

I этап. Проверка домашнего задания. Теоретический опрос

Цель деятельности

Деятельность учителя

Деятельность учащихся

Проверить уровень усвоения формул для нахождения площади треугольника

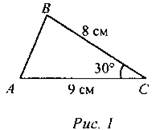
(Ф/И)

- Сформулируйте и докажите теорему о площади треугольника.

- Выведите формулу для вычисления площади прямоугольного треугольника.

- Докажите, что если высоты двух треугольников равны, то их площади соотносятся как основания.

(И) - Решите задачи с последующей самопроверкой.

Найти: S_АВС.

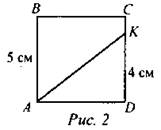
ABCD - квадрат, AB = 5 см, KD = 4 см.

Найти: S_ABCK.

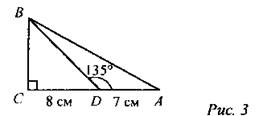
AB = 10.

Найти: S_BCA.

Ответ: 36 см².

Ответ: 15 см².

Ответ: 60 см²

II этап. Мотивация к деятельности

Цель деятельности

Совместная деятельность

Через решение задач подготовить учащихся к восприятию новой теоремы

(Ф)

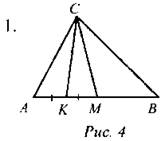
СМ - медиана ∆АВС, СК - медиана ∆ACM.

Найти: S_ACM : S_ABC; S_ACM : S_BCK; S_ACK : S_BCK.

Ответ:

M - середина АВ, К - середина CD. ABCD - выпуклый четырехугольник.

Доказать: S_MBKD = S_ABCD : 2.

Доказательство: S_ADB : S_MDB = 2 : 1; S_DCB : S_DKB = 2 : 1; S_ABCD = S_ADB + S_DBC, S_MDKB = S_MDB + S_DKB; S_ABCD : S_MDKB = 2 : 1

III этап. Изучение новой темы

Цель деятельности

Совместная деятельность

Доказать теорему об отношении площадей треугольников, имеющих по равному углу

(Ф) Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы. (Доказывает сам учитель.)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

На примерах отработать применение данной теоремы

(Ф)

1. Дано: ∠А = ∠К, АС = 5 см, АВ = 3 см, KN = 7 см, КМ = 2 см.

Найти: S_ABC : S_KMN.

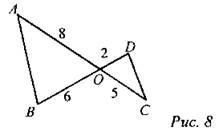
2. Дано: ОА = 8 см, ОБ = 6 см, ОС = 5 см, OD = 2 см, S_AOB = 20 см².

Найти: S_COD.

(И) Решить самостоятельно задачу.

Площадь одного равностороннего треугольника в 3 раза больше, чем площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.

Решить самостоятельно задачу № 479 (б)

1. Решение:

2. Решение:

Проверка:

Самостоятельная работа обучающего характера

Цель деятельности

Задания для самостоятельной работы

Проверить уровень понимания доказанной теоремы

(И)

Вариант I

1. Две стороны треугольника равны 12 см и 9 см, а угол между ними 30°. Найдите площадь треугольника.

2.

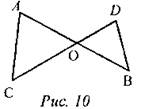
Дано: АО = 4; ВО = 9; СО = 5; DO = 8. S_AOC = 15.

Найти: S_BOD.

Вариант II

1. Найдите площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 30°.

2.

Дано: АО = 10; СО = 12; DO = 6; ВО = 8, S_BOD = 14.

Найти: S_AOC.

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И) - Продолжите фразы:

• Сегодня на уроке я узнал...

• Мне было труднее всего...

• Самым полезным для меня было...

(И) Домашнее задание: решить задачи № 479 (а), 476 (а), 477