Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Контрольная работа № 9 по теме Системы линейных уравнений - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, опенки и коррекции знаний.
Ход урока
I. Сообщение темы и цели урока
II. Общая характеристика контрольной работы
Контрольная работа составлена в шести вариантах (варианты 1, 2 — самые простые, варианты 3, 4 — средней сложности, варианты 5, 6 — самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка “3” ставится за любые три решенные задачи, оценка “4” — за четыре задачи и оценка “5” — за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5, 6 — дополнительно 1 балл (т. е. оценка “5” выставляется уже за четыре задачи). Все задачи в варианте примерно равноценны. Возможно, несколько труднее для учеников задачи 5, 6.
Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов.
Контрольная работа рассчитана на один урок.
III. Контрольная работа
Вариант 1
1. Из пар чисел (-2; 1), (2; -1), (1; 2) выберите решение системы линейных уравнений ![]()
2. Решите систему линейных уравнений ![]() графическим способом.
графическим способом.
3. Решите систему уравнений ![]() способом подстановки.
способом подстановки.
4. Решите систему уравнений ![]() способом сложения.
способом сложения.
5. Прямая у = kx + b проходит через точки А (2; 7) и В (-1; -2). Найдите величины k и b.
6. Пять досок и шесть брусьев весят 107 кг. Четыре доски тяжелее двух брусьев на 4 кг. Сколько весит одна доска и один брус?
Вариант 2
1. Из пар чисел (-2; 1), (-1; 2), (1; 2) выберите решение системы линейных уравнений ![]()
2. Решите систему линейных уравнений ![]() графическим способом.
графическим способом.
3. Решите систему уравнений ![]() способом подстановки.
способом подстановки.
4. Решите систему уравнений ![]() способом сложения.
способом сложения.
5. Прямая у = kх + b проходит через точки А (2; 7) и В (-1; 1). Найдите величины k и b.
6. Семь досок и три кирпича вместе весят 71 кг. Три доски тяжелее двух кирпичей на 14 кг. Сколько весит одна доска и один кирпич?
Вариант 3
1. Из пар чисел (-2; 1), (3; -1), (2; -2) выберите решение системы нелинейных уравнений ![]()
2. Решите систему нелинейных уравнений ![]() графическим способом.
графическим способом.
3. Решите систему уравнений ![]() способом подстановки.
способом подстановки.
4. Прямая у = kх + b проходит через точки А (-1; -5) и В (2; 4). Найдите величины k и b.
5. При всех значениях параметра а определите число решений системы уравнений ![]()
6. Решите уравнение 4х2 - 12ху + 9у2 + 5|х - 2у + 3| = 0.
Вариант 4
1. Из пар чисел (-2; 1), (3; -2), (2; -2) выберите решение системы нелинейных уравнений ![]()
2. Решите систему нелинейных уравнении ![]() графическим способом.
графическим способом.
3. Решите систему уравнений ![]() способом подстановки.
способом подстановки.
4.Прямая у = kх + b проходит через точки А (-2; 4) и В (1; -5). Найдите величины k и b.
5. При всех значениях параметра а определите число решений системы уравнений ![]()
6. Решите уравнение 9х2 + 12ху + 4у2 + 5|3х – у - 6| = 0.
Вариант 5
1. Система уравнений ![]() имеет решение (2; 1). Найдите числа a и b.
имеет решение (2; 1). Найдите числа a и b.
2. Решите систему уравнений 
3. Решите систему уравнений ![]() графическим способом.
графическим способом.
4. Прямые у = 3 - х, у = 2х, у = ах - 2 пересекаются в одной точке. Найдите коэффициент а.
5. Катер прошел путь по течению реки от пункта А до пункта В за 6 ч, а обратный путь — за 8 ч. За сколько часов плот преодолеет путь от пункта А до пункта В?
6. При всех значениях параметра а определите число решений системы ![]()
Вариант 6
1. Система уравнений ![]() имеет решение (1; 2). Найдите числа а и b.
имеет решение (1; 2). Найдите числа а и b.
2. Решите систему уравнений 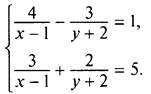
3. Решите систему уравнений ![]() графическим способом.
графическим способом.
4. Прямые ![]() пересекаются в одной точке. Найдите коэффициент а.
пересекаются в одной точке. Найдите коэффициент а.
5. Катер прошел путь по течению реки от пункта А до пункта В за 4 ч, а обратный путь — за 6 ч. За сколько часов плот преодолеет путь от пункта А до пункта В?
6. При всех значениях параметра а определите число решений системы ![]()
IV. Подведение итогов контрольной работы
1. Распределение работ по вариантам и результаты решения. Удобно данные заносить в таблицу (для каждой пары вариантов).
|
№ задачи |
Итоги |
|||
|
+ |
± |
- |
Ø |
|
|
1 |
5 |
1 |
1 |
1 |
|
2 |
||||
|
... |
||||
|
6 |
||||
Обозначения:
+ — число решивших задачу правильно или почти правильно;
± — число решивших задачу со значительными погрешностями;
- — число не решивших задачу;
Ø — число не решавших задачу.
Варианты 1, 2 — 8 учащихся.
2. Типичные ошибки при решении задач.
3. Задачи, вызвавшие наибольшие трудности.
V. Разбор задач (ответы и решения)
Вариант 1
1. (2; -1).
2. (2; 4).
3. (2; 1).
4. (2; 2).
5. у = 3х + 1.
6. Масса доски 7 кг, бруса - 12 кг.
Вариант 2
1. (-1; 2).
2. (2; 2).
3. (1; 2).
4. (1; -1).
5. у = 2х + 3.
6. Масса доски 8 кг, кирпича - 5 кг.
Вариант 3
1. (3; -1).
2. (-1; 0), (0; -1), (1; 0).
3. (-19; -3).
4. у = 3х - 2.
5. При а ≠ 2,5 единственное решение, при а = 2,5 решений нет.
6. (9; 6).
Вариант 4
1. (3; -2).
2. (-1; 1), (1; 1).
3. (7; 4).
4. у = -3х - 2.
5. При а ≠ 1,5 единственное решение, при а = 1,5 бесконечно много решений.
6. (4/3; -2).
Вариант 5
1. Подставим данное решение (2; 1) в систему уравнений ![]() и получим систему линейных уравнений для определения величин а и b:
и получим систему линейных уравнений для определения величин а и b: ![]() или
или ![]()
Решим эту систему способом подстановки. Из первого уравнения выразим b = 11 - 2а и подставим это выражение во второе уравнение. Получаем линейное уравнение с одним неизвестным: -а + 2(11 - 2а) = 7, или -а + 22 - 4а = 7, или -5а = -15, откуда а = 3. Используя формулу b = 11 - 2а, найдем b = 11 – 2 ∙ 3 = 11 - 6 = 5.
(Ответ: а = 3, b = 5.)
2. Систему уравнений ![]() запишем в виде
запишем в виде ![]()
Построим графики функций у = |х + 1| (ломаная 1) и у = 1 - |х| (ломаная II). Видно, что графики совпадают по отрезку АВ. Следовательно, данная система имеет бесконечно много решений. Запишем их. Отрезок АВ расположен на прямой у = х + 1, при этом абсцисса любой точки отрезка АВ удовлетворяет условию -1 ≤ х ≤ 0. Поэтому решением данной системы будут пары чисел (х; у), в которых -1 ≤ х ≤ 0 и у = х + 1.
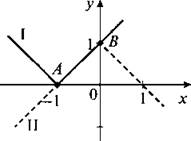
(Ответ: -1 ≤ х ≤ 0, у = х + 1.)
3. Система уравнений 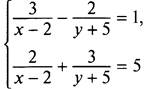 нелинейная. Однако при ее решении также можно использовать способ сложения. Для этого перед слагаемыми, зависящими от у, коэффициенты сделаем противоположными. Умножим первое уравнение почленно на число 3, второе уравнение — на число 2. Получаем систему уравнений
нелинейная. Однако при ее решении также можно использовать способ сложения. Для этого перед слагаемыми, зависящими от у, коэффициенты сделаем противоположными. Умножим первое уравнение почленно на число 3, второе уравнение — на число 2. Получаем систему уравнений 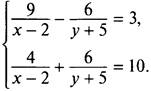
Сложим почленно левые и правые части уравнений системы и получим уравнение с одним неизвестным: ![]() или
или ![]()
Тогда знаменатель дроби х - 2 = 1, откуда х = 3. Подставим это значение, например, в первое уравнение и получим ![]() или
или ![]() или
или ![]()
Тогда знаменатель дроби у + 5 = 1, откуда у = -4. Итак, система имеет единственное решение (3; -4).
(Ответ: (3; -4).)
4. Пусть данные прямые пересекаются в точке А (х0; у0). Тогда координаты этой точки удовлетворяют уравнениям прямых. Получаем систему уравнений с параметром а:
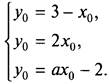
Первые два уравнения не содержат параметра а. Поэтому сначала решим систему, образованную этими уравнениями: ![]()
Для ее решения используем еще один способ — способ сравнения. Так как в этих уравнениях равны левые части, то можно приравнять и правые. Получаем линейное уравнение с одним неизвестным: 3 - x0 = 2x0 или 3 = 3х0, откуда x0 = 1.
Из первого уравнения этой системы находим у0 = 3 - 1 = 2.
Итак, первые две прямые пересекаются в точке А (1; 2). Подставим найденные значения х0 и у0 в третье уравнение данной системы и получим 2 = а ∙ 1 - 2 или 2 = а - 2, откуда а = 4.
(Ответ: а = 4.)
5. Пусть расстояние между пунктами А и В равно S км, собственная скорость катера (скорость в стоячей воде) равна х км/ч, а скорость течения реки — у км/ч. При движении по течению реки скорость катера увеличивается и равна х + у км/ч. За 6 ч катер, двигаясь с такой скоростью, проходит расстояние (х + у) ∙ 6, равное S. Получаем первое уравнение: 6(х + у) = S. При движении против течения реки скорость катера уменьшается и равна х - у км/ч. За 8 ч катер, двигаясь с такой скоростью, проходит расстояние (х - у) ∙ 8, равное S. Имеем второе уравнение: 8(х - у) = S.
Получим систему уравнений ![]() или
или ![]()
Особенность этой системы в том, что в нее входят три неизвестных и два уравнения и найти эти неизвестные нельзя. Плот может двигаться только со скоростью реки у км/ч. Поэтому способом сложения исключим из данной системы переменную х. Для этого умножим почленно первое уравнение на число 4, второе уравнение — на число -3. Получаем равносильную систему уравнений ![]()
Сложим почленно левые и правые части уравнений системы и получим 24у + 24у = 4S – 3S или 48у = S.
Плот пройдет расстояние S со скоростью у за время ![]()
(Ответ: за 48 ч.)
6. Для системы уравнений ![]() запишем условие единственности решения:
запишем условие единственности решения: ![]() или а2 – 1 ≠ 0, или (а - 1)(а + 1) ≠ 0, откуда а ≠ 1 и а ≠ -1. При а ≠ ±1 система имеет единственное решение. Определим число решений системы при а = -1 и а = 1. Подставим значение а = -1 в данную систему и получим
или а2 – 1 ≠ 0, или (а - 1)(а + 1) ≠ 0, откуда а ≠ 1 и а ≠ -1. При а ≠ ±1 система имеет единственное решение. Определим число решений системы при а = -1 и а = 1. Подставим значение а = -1 в данную систему и получим ![]() или
или ![]()
Умножим первое уравнение почленно на число -1. Получаем равносильную систему уравнений ![]()
Очевидно, что такая система решений не имеет, так как одна и та же величина х - у из первого уравнения равна 1, из второго уравнения — равна -1.
Подставим значение а = 1 в данную систему и получим ![]() или
или ![]()
Такая система уравнений имеет бесконечно много решений, так как уравнения системы одинаковы.
(Ответ: при а ≠ ±1 единственное решение, при а = -1 решений нет, при а = 1 бесконечно много решений.)
Вариант 6
1. Подставим данное решение (1; 2) в систему уравнений ![]() и получим систему линейных уравнений для определения величин а и b:
и получим систему линейных уравнений для определения величин а и b: ![]() или
или ![]()
Решим эту систему способом подстановки. Из первого уравнения выразим а = 7 – 2b и подставим это выражение во второе уравнение. Получаем линейное уравнение с одним неизвестным: 6(7 – 2b) + 2b = 22, или 42 - 12b + 2b = 22, или -10b = -20, откуда b = 2. Используя формулу а = 7 – 2b, найдем а = 7 - 2 ∙ 2 = 7 - 4 = 3.
(Ответ: а = 3, b = 2.)
2. Систему уравнений ![]() запишем в виде
запишем в виде ![]()
Построим графики функций у = |х - 1| (ломаная I) и у = |х| - 1 (ломаная II). Видно, что графики совпадают по лучу АВ. Следовательно, данная система имеет бесконечно много решений. Запишем их. Луч АВ расположен на прямой у = х - 1, при этом абсцисса любой точки луча АВ удовлетворяет условию х ≥ 1. Поэтому решением данной системы будут пары чисел (х, у), в которых х ≥ 1 и у = х - 1.
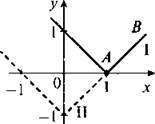
(Ответ: х ≥ 1, у = х - 1.)
3. Система уравнений 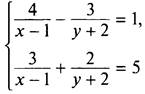 нелинейная. Однако при ее решении также можно использовать способ сложения. Для этого перед слагаемыми, зависящими от у, коэффициенты сделаем противоположными. Умножим первое уравнение почленно на число 2, второе уравнение — на число 3. Получаем систему уравнении
нелинейная. Однако при ее решении также можно использовать способ сложения. Для этого перед слагаемыми, зависящими от у, коэффициенты сделаем противоположными. Умножим первое уравнение почленно на число 2, второе уравнение — на число 3. Получаем систему уравнении 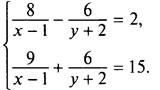
Сложим почленно левые и правые части уравнений системы и получим уравнение с одним неизвестным: ![]() или
или ![]()
Тогда знаменатель дроби х - 1 = 1, откуда х = 2. Подставим это значение, например, в первое уравнение: ![]() или
или ![]() или
или ![]()
Тогда знаменатель дроби у + 2 = 1, откуда у = -1. Итак, система имеет единственное решение (2; -1).
(Ответ: (2; -1).)
4. Пусть данные прямые пересекаются в точке А (х0; у0). Тогда координаты этой точки удовлетворяют уравнениям прямых. Получаем систему уравнений с параметром а:
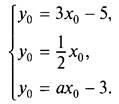
Первые два уравнения не содержат параметра а. Поэтому сначала решим систему, образованную этими уравнениями:
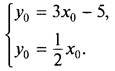
Для ее решения используем еще один способ — способ сравнения. Так как в этих уравнениях равны левые части, то можно приравнять и правые. Получаем линейное уравнение с одним неизвестным: ![]() или 6х0 - 10 = х0, откуда х0 = 2.
или 6х0 - 10 = х0, откуда х0 = 2.
Из первого уравнения этой системы находим у0 = 3 ∙ 2 - 5 = 6 - 5 = 1.
Итак, первые две прямые пересекаются в точке А (2; 1). Подставим найденные значения х0 и у0 в третье уравнение данной системы и получим 1 = а ∙ 2 - 3 или 1 = 2а - 3, откуда а = 2.
(Ответ: а = 2.)
5. Пусть расстояние между пунктами А и В равно S км, собственная скорость катера (скорость в стоячей воде) равна х км/ч, а скорость течения реки - у км/ч. При движении по течению реки скорость катера увеличивается и равна х + у км/ч. За 4 ч катер, двигаясь с такой скоростью, проходит расстояние (х + у) ∙ 4, равное S. Получаем первое уравнение: 4(х + у) = S. При движении против течения реки скорость катера уменьшается и равна х - у км/ч. За 6 ч катер, двигаясь с такой скоростью, проходит расстояние (х - у) ∙ 6, равное S. Имеем второе уравнение: 6(х - у) = S.
Получим систему уравнении ![]() или
или ![]()
Особенность этой системы в том, что в нее входят три неизвестных и два уравнения и найти эти неизвестные нельзя. Плот может двигаться только со скоростью реки у км/ч. Поэтому способом сложения исключим из этой системы переменную х. Для этого умножим почленно первое уравнение на число 3, второе уравнение — на число -2. Получаем равносильную систему уравнений: ![]()
Сложим почленно левые и правые части уравнений системы и получим 12у + 12у = 3S – 2S или 24у = S. Плот пройдет расстояние S со скоростью у за время ![]()
(Ответ: за 24 ч.)
6. Для системы уравнений ![]() запишем условие единственности решения:
запишем условие единственности решения: ![]() или 1 ≠ а2, или 0 ≠ а2 - 1, или 0 ≠ (а - 1)(а + 1), откуда а ≠ 1 и а ≠ -1. При а ≠ ±1 система имеет единственное решение. Определим число решений системы при а = -1 и а = 1. Подставим значение а = -1 в данную систему и получим
или 1 ≠ а2, или 0 ≠ а2 - 1, или 0 ≠ (а - 1)(а + 1), откуда а ≠ 1 и а ≠ -1. При а ≠ ±1 система имеет единственное решение. Определим число решений системы при а = -1 и а = 1. Подставим значение а = -1 в данную систему и получим ![]() или
или ![]()
Умножим второе уравнение почленно на число -1. Получаем равносильную систему уравнении ![]()
Очевидно, что такая система решений не имеет, так как одна и та же величина х - у из первого уравнения равна 1, из второго уравнения — равна -1.
Подставим значение а = 1 в данную систему и получим ![]() или
или ![]()
Такая система уравнений имеет бесконечно много решений, так как уравнения системы одинаковы.
(Ответ: при а ≠ ±1 единственное решение, при а = -1 решений нет, при а = 1 бесконечно много решений.)
VI. Подведение итогов урока