Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Возведение в куб суммы и разности двух выражений - КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цель: вывести формулы для возведения в куб суммы или разности чисел (выражений).
Планируемые результаты: научиться пользоваться формулами куба суммы и куба разности.
Тип уроков: уроки общеметодологической направленности.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Сформулируйте словами, как найти квадрат суммы, и запишите соответствующую формулу.
2. Представьте в виде многочлена:
![]()
3. Упростите выражение ![]() и найдите его значение при b = 1/2.
и найдите его значение при b = 1/2.
4. Найдите значение выражения ![]()
Вариант 2
1. Сформулируйте словами, как найти квадрат суммы, и запишите соответствующую формулу.
2. Представьте в виде многочлена:
![]()
3. Упростите выражение ![]() и найдите его значение при а = -1/2.
и найдите его значение при а = -1/2.
4. Найдите значение выражения ![]()
III. Работа по теме уроков
Приведем еще две формулы сокращенного умножения, позволяющие возводить в куб сумму или разность двух чисел (выражений).
![]()
Тождество (1) называют формулой куба суммы. В соответствии с ней куб суммы двух чисел (выражений) равен кубу первого числа (выражения) плюс утроенное произведение квадрата первого числа (выражения) и второго плюс утроенное произведение первого числа (выражения) и квадрата второго плюс куб второго числа (выражения).
Получим формулу (1) алгебраическим способом.
Используя свойства степеней и формулу квадрата суммы, получаем
![]()
Заметим, что формула (1) может быть получена и геометрическим способом. Для этого необходимо рассмотреть объемы параллелепипедов.
Формула куба разности имеет аналогичный вид:
![]()
В соответствии с формулой (2) куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения.
Формулу (2) можно вывести аналогично формуле (1):
![]()
Заметим, что формула (2) может быть непосредственно получена из формулы (1):
![]()
![]()
Пример 1
Возведем в куб число 101.
Используя формулу (1), получаем
![]()
Пример 2
Возведем в куб число 99.
Используя формулу (2), получаем ![]()
![]()
Пример 3
Возведем в куб двучлен 2а + 3b.
Используя формулу (1), получаем
![]()
Пример 4
Возведем в куб двучлен а3 – 2b2.
Используя формулу (2), получаем
![]()
Пример 5
Упростим выражение ![]()
Используя формулу (2) и раскрыв скобки, получаем ![]()
![]()
Заметим, что формулы (а + b)2 и (а + b)3, (а - b)2 и (а - b)3 являются частными случаями формул (а + b)n и (а - b)n для n = 2 и n = 3 (бином Ньютона). Поэтому существуют определенные закономерности в этих формулах. Приведем еще раз формулы (а + b)n и (а - b)n для n = 1, 2, 3.
|
n |
(а + b)n |
(а - b)n |
|
1 |
а + b |
а - b |
|
2 |
а2 + 2ab + b2 |
а2 - 2ab + b2 |
|
3 |
а3 + 3а2b + 3аb2 + b3 |
а3 - 3а2b + 3аb2 - b3 |
Отметим закономерности этих формул:
1. При возведении суммы или разности двух чисел в n-ю степень получается однородный многочлен n-й степени, т. е. многочлен, состоящий из одночленов только n-й степени. Количество членов в многочлене равно n + 1. Например, при возведении а + b в квадрат получается однородный многочлен второй степени, состоящий из трех членов.
2. Получающийся однородный многочлен начинается с аn. В следующем члене степень а уменьшается на единицу, но появляется множитель b. В следующем члене опять степень а уменьшается на единицу, степень b увеличивается на единицу и так до тех пор, пока степень b не будет равна n.
3. При такой записи получающегося многочлена крайние члены имеют коэффициенты 1, остальные члены — коэффициенты n (только при n = 2, 3). Например, при возведении в куб суммы а + b коэффициенты последовательно равны 1, 3, 3, 1.
4. При возведении в п-ю степень суммы а + b все коэффициенты имеют знак “плюс”. При возведении разности а - b знаки коэффициентов чередуются, начиная со знака “плюс”.
Например, при возведении разности а - b в куб коэффициенты последовательно равны 1, -3, 3, -1.
5. Все сказанное справедливо только при n = 1, 2, 3. Начиная с n = 4 закономерности становятся сложнее.
IV. Задания на уроках и на дом
1. Используя соответствующие формулы, найдите:
а) 313;
б) 283;
в) 523;
г) 493.
Ответы: а) 29 791; б) 21 952; в) 140 608; г) 117 649.)
2. Вычислите:

(Ответы:

3. Решите уравнение:
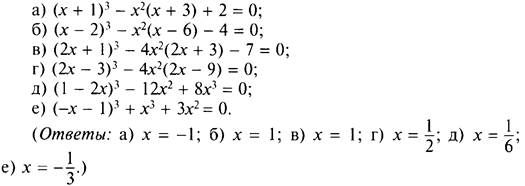
V. Контрольные вопросы
— Сформулируйте словами, как найти куб суммы, и запишите соответствующую формулу.
— Выведите формулу куба суммы алгебраическим способом.
— Сформулируйте словами, как найти куб разности, и запишите соответствующую формулу.
— Выведите формулу куба разности алгебраическим способом.
VI. Подведение итогов уроков