Возведение в квадрат суммы и разности двух выражений - КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ

Цель: вывести формулы для возведения в квадрат суммы и разности выражений.

Планируемые результаты: научиться пользоваться формулами квадрата суммы и квадрата разности.

Тип урока: урок проблемного изложения.

Ход урока

I. Сообщение темы и цели урока

II. Работа по теме урока

При перемножении многочленов и приведении их к стандартному виду, а также при решении многих других задач очень полезными оказываются формулы сокращенного умножения.

Прежде всего, рассмотрим формулы для возведения в квадрат суммы и разности двух выражений.

(квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения);

(квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения).

Тождество (1) называют формулой квадрата суммы, тождество (2) — формулой квадрата разности. Эти формулы позволяют возводить в квадрат сумму или разность любых двух чисел (выражений). Формулы (1) и (2) можно получить алгебраическим и геометрическим способами.

Выведем формулу

Алгебраический способ

По определению Перемножим эти многочлены:

Геометрический способ

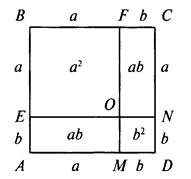
Рассмотрим квадрат ABCD со стороной а + b. Очевидно, что его площадь равна (а + b)². Теперь на расстоянии а от вершины В проведем прямые EN и FM, параллельные сторонам квадрата. Эти прямые разбили нашу фигуру на квадрат BFOE (со стороной а и площадью а²), квадрат OMDN (со стороной b и площадью b²) и два прямоугольника АЕОМ и FONC (со сторонами а и b и площадью ab).

Так как эти четыре фигуры полностью расположены внутри исходного квадрата, то сумма их площадей а² + b² + 2ab равна площади большого квадрата (а + b)². Поэтому получаем

Заметим, что формула квадрата суммы была получена древнегреческими математиками еще до нашей эры (более 2000 лет назад) именно геометрическим способом. Видно, что применение алгебры позволяет значительно упростить и ускорить вывод формул.

Теперь выведем формулу

Алгебраический способ

По определению Перемножим эти многочлены:

Приведем подобные члены и получим

Заметим, что эту формулу можно вывести и из формулы (1), заменив операцию вычитания операцией сложения: a - b = a + (-b). Тогда получаем

Геометрический способ

Будем считать, что а > b. Рассмотрим квадрат A BCD со стороной а. Очевидно, что его площадь равна а².

Теперь на расстоянии b от вершины В проведем прямые EN и FM, параллельные сторонам квадрата. Эти прямые разбили фигуру на квадрат В FOE (со стороной b и площадью b²), квадрат OMDN(со стороной а - b и площадью (а - b)²) и два прямоугольника ABFM и BCNE (со сторонами а и b и площадью ab).

Площадь квадрата OMDN (равную (а - b)²) найдем, если из площади квадрата ABCD (равной а²) вычтем площади двух прямоугольников ABFM и BCNE (каждая из которых равна ab) и добавим площадь квадрата BFOE (равную b²). В итоге получаем

Рассмотрим примеры применения формул квадрата суммы и квадрата разности.

Пример 1

Возведем в квадрат число 52.

Запишем число 52 в виде 52 = 50 + 2 и используем формулу квадрата суммы:

Пример 2

Возведем в квадрат число 49.

Запишем число 49 в виде 49 = 50 - 1 и используем формулу квадрата разности:

Пример 3

Возведем в квадрат сумму 5а + 3b. По формуле квадрата суммы получаем

Пример 4

Возведем в квадрат разность 7а – 2b. По формуле квадрата разности имеем

Пример 5

Докажем, что выражение не зависит от а, и найдем величину А.

Запишем выражение А в виде

Очевидно, что выражение A является квадратом разности чисел (а - 4) и (а + 8). Получаем

Действительно, выражение А не зависит от а; А = 144.

Пример 6

Упростим выражение

Используем формулу квадрата суммы, раскроем скобки и приведем подобные члены. Получаем

III. Задания на уроке

№ 799 (а, г, д), 803 (б, в), 806 (а), 810 (в, г), 812 (а, б), 814 (а, в), 818 (в, г), 823 (в), 824 (б).

IV. Контрольные вопросы

— Сформулируйте словами, как найти квадрат суммы, и запишите соответствующую формулу.

— Выведите формулу квадрата суммы алгебраическим способом, а затем геометрическим способом.

— Сформулируйте словами, как найти квадрат разности, и запишите соответствующую формулу.

— Выведите формулу квадрата разности алгебраическим способом, а затем геометрическим способом.

V. Подведение итогов урока

Домашнее задание

№ 799 (б, в, е), 803 (а, е), 806 (б), 810 (д, е), 812 (г, д), 814 (б, г), 818 (а, б), 823 (г), 824 (г).