Алгебра 7 класс - Технологические карты уроков по учебнику А. Г. Мордковича - 2016
Урок 6. ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ - МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
|
Тип урока: закрепление нового материала |
|||||
|
Задачи: создать условия для развития умений решать текстовые задачи, выделяя три этапа математического моделирования |
|||||
|
Планируемые результаты |
|||||
|
Предметные: научатся решать текстовые задачи, используя разные виды математических моделей |
Метапредметные: познавательные - ориентироваться на разнообразие способов решения задач; регулятивные - учитывать правило в планировании и контроле способа решения; коммуникативные - учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Личностные: развивать познавательный интерес к математике |
|||
|
Образовательные ресурсы: 1) Уроки по основным предметам школьной программы. URL: http://intemeturok.ru/ru 2) Школьный помощник. URL: http://school-assistant.ru/ |
|||||
|
Организационная структура урока |
|||||
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности |
||
|
1. Организационный этап |
|||||
|
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся |
|||||
|
3. Проверка домашнего задания |
|||||
|
4. Актуализация знаний |
Фронтальный опрос по теоретическому материалу темы “Что такое математическая модель” РМ |
Отвечают на вопросы |
Умение работать по заданному алгоритму, доказывать правильность решения с помощью аргументов |
||
|
5. Закрепление изученного материала |
Организует индивидуальную работу для учащихся, которые освоили тему: составить карточки |
У доски: № 3.33-3.37. Индивидуально: № 3.43-3.45 |
|||
|
6. Повторение |
Задачник: № 2.19 |
||||
|
7. Контроль и коррекция знаний |
Дает консультацию по решению заданий, но не решает само задание |
Обучающая самостоятельная работа в двух вариантах РМ |
|||
|
8. Итоги урока |
Фронтальный опрос по теории (вопросы для самопроверки) |
Поиск ответов к вопросам для самопроверки (учебник, § 3) |
|||
|
9. Домашнее задание |
Задачник: № 3.31, 3.41, 3.40, 3.45 |
Творческое задание РМ |
|||
Ресурсный материал к уроку 6
1. Фронтальный опрос.
Если количество бананов х, количество апельсинов у, составить математическую модель ситуации:
• количество бананов равно количеству апельсинов;
• количество бананов в 2 раза больше количества апельсинов;
• бананов и апельсинов 7 штук;
• стоимость 3 бананов равна 12 рублям;
• апельсинов больше бананов на 4 штуки;
• стоимость 2 апельсинов равна 18 рублям;
• если съесть 1 банан и 3 апельсина, то количество фруктов равняется.
2. Обучающая самостоятельная работа.
|
Вариант I |
Вариант II |
|
1. Найдите значение числового выражения: 2. Найдите значение алгебраического выражения: а) (5х - у)(3у + х) при х = 7, у = -5; б) 3. Запишите на математическом языке произведение суммы чисел а и b и куба числа с. 4. Решите уравнение: (9x - 7) - (6 + 7х) = 5. 5. Решите уравнение: 0,8(3 + x) = 23,7 + 0,7(x - 5). 6. Составьте математическую модель ситуации: Теплоход проплыл против течения реки за t часов 53 км. Скорость течения реки 1,3 км/ч. Скорость теплохода в стоячей воде v км/ч. Найдите значение t, если v = 27,8 км/ч |
1. Найдите значение числового выражения: 2. Найдите значение алгебраического выражения: а) (7n + m)(4m - n) при n = -3, m = 2; б) 3. Запишите на математическом языке разность произведения чисел х и у и квадрата числа z. 4. Решите уравнение: (13а + 7) - (10а - 4) = 17. 5. Решите уравнение: 0,4(x + 8) - 4,7 = 0,3(x - 3). 6. Составьте математическую модель ситуации: Теплоход проплыл по течению реки за t часов 36 км. Скорость течения реки v км/ч. Скорость теплохода в стоячей воде 9,8 км/ч. Найдите значение t, если v = 2,2 км/ч |
Ответы к обучающей самостоятельной работе:
|
Задание |
1 |
2(a) |
2(6) |
3 |
4 |
5 |
6 |
|
Вариант I |
1,975 |
-320 |
2,5 |
(а + b) ∙ с3 |
9 |
178 |
|
|
Вариант II |
12 |
-209 |
16 |
xy - z2 |
2 |
6 |
|
3. Творческое задание. Из двух городов, расстояние между которыми равно 270 км, выехали одновременно навстречу друг другу два автомобиля. Через 2 ч после начала движения расстояние между ними составило 30 км. Найдите скорость каждого автомобиля, если скорость одного из них на 10 км/ч больше скорости другого.
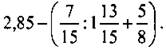
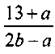 при а = 12, b = 11.
при а = 12, b = 11.