Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Прямоугольный параллелепипед - ПЛОЩАДИ И ОБЪЕМЫ - НАТУРАЛЬНЫЕ ЧИСЛА
Основная дидактическая цель урока: познакомить учащихся с геометрическим телом на примере прямоугольного параллелепипеда; учить решать задачи на нахождение площади поверхности прямоугольного параллелепипеда.
Ход урока
I. Организационный момент
II. Устный счет. Определение темы урока
— Решив примеры и заполнив таблицу, вы сможете узнать тему урока.

909
600
0
600
16
16
240
16
240
909
385
909
240
100
— Какое слово у вас получилось?
— Это и будет темой нашего урока.
— Что означает это слово?
III. Работа по теме урока
1. С. 120—121 (работа по статье учебника).
— Прочитайте статью учебника и приготовьтесь отвечать на вопросы.
2. Работа в тетради.
(Для того чтобы учащиеся научились правильно видеть все элементы прямоугольного параллелепипеда, надо научить их изображать его схематически.)
1) Начертите прямоугольник.
2) Из его вершин в одном направлении и под одним углом проведите равные отрезки.
3) Концы отрезков соедините между собой.
4) Отрезки, которые обозначают невидимые ребра, ластиком превратим в пунктирные линии.
5) Прямоугольный параллелепипед готов.
(Учитель показывает на доске.)
6) Обозначьте вершины латинскими буквами.
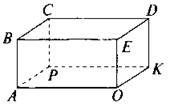
3. Ответьте на вопросы (устно).
— Назовите грань, на которой стоит параллелепипед.
— Назовите грань, которая лежит напротив. Такие грани называются противоположными.
— Назовите еще пары противоположных граней.
— Что вы можете о них сказать?
— Что можете сказать об их площадях?
— Если мы найдем сумму площадей всех граней, это значит, мы узнаем площадь всей поверхности прямоугольного параллелепипеда.
— Назовите ребра, которые “сходятся” в вершине О. Какое из них может быть длиной, шириной и высотой?
4. А теперь решим такую задачу.
Найдите площадь поверхности нашего прямоугольного параллелепипеда, если три его измерения равны 6 см, 5 см и 3 см. (Для лучшего понимания на рисунке добавляются размеры.)
— Как найти площадь грани, на которой параллелепипед стоит? Сколько таких граней?
2S1 = 6 ∙ 5 ∙ 2 = 60 (см2)
Аналогично с другими гранями.
2S2 = 6 ∙ 3 ∙ 2 = 36 (см2)
2S3 = 5 ∙ 3 ∙ 2 = 30 (см2)
Sповерхности =60 + 36 + 30= 126 (см2)
IV. Работа по учебнику
С. 121—122, № 792 (прочитать объяснение).
Вариант 1 (а)
Выполните рисунок и решите задачу.
S = 6 ∙ 8 ∙ 2 + 6 ∙ 4 ∙ 2 + 8 ∙ 4 ∙ 2 = 96 + 48 + 64 = 208 (см2)
Вариант 2 (б)
S = 2 ∙ 3 ∙ 2 + 2 ∙ 11 ∙ 2 + 3 ∙ 11 ∙ 2 = 12 + 44 + 66 = 122 (см2)
V. Работа над задачами
1. С. 122, № 793.
— Выполните рисунок.
— Назовите размеры бака.
— Что нужно узнать в задаче?
— Как изменится площадь поверхности, если сказано, что бак нужно покрасить и снаружи, и изнутри?
— Как повлияет на решение информация о том, что бак без крышки?
Sоснования = 90 ∙ 50 = 4500 (см2)
Sбоковая = 90 ∙ 70 ∙ 2 + 50 ∙ 70 ∙ 2 = 19600 (см2)
Sобщ = 4500 + 19 600 = 24 100 (см2)
24 100 ∙ 2 = 48 200 см2 = 482 (дм2) — площадь бака снаружи и изнутри.
2. С. 122, № 794 (интерактивное пособие).
Sбоковая = 50 ∙ 30 ∙ 2 + 25 ∙ 30 ∙ 2 = 3000 + 1500 = 4500 (см2)
VI. Рефлексия
— Какое геометрическое тело мы сегодня изучали?
— Что вы запомнили?
Домашнее задание
С. 124, № 813, 814.