Контрольные и самостоятельные работы по математике 5 класс - С. Г. Журавлев - 2015
Формулы площади и объема (домашняя самостоятельная работа) - ПЛОЩАДИ И ОБЪЕМЫ - САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
С20*. Формулы площади и объема (домашняя самостоятельная работа)
Вариант 1
1. Найдите площадь окрашенной части квадрата.
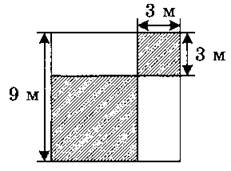
2. Пусть одна тетрадная клетка изображает участок площадью 50 м2. Изобразите прямоугольный участок площадью 5а.
3. Сколько квадратов изображено на рисунке?
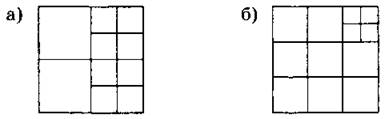
4. Прямоугольник разрезали на квадраты (см. рис.). Сторона наибольшего квадрата равна 12 см. Найдите периметр и площадь прямоугольника.
5. а) Сколько квадратов, равных данному, надо взять, чтобы сложить из них квадрат со стороной в 4 раза больше, чем сторона данного квадрата?
б) Сколько кубов, равных данному, надо взять, чтобы сложить из них куб, со стороной в 4 раза больше, чем сторона данного куба?
6. Прямоугольный параллелепипед с размерами 3 м, 4 м, 6 м разрезали на кубические дециметры и поставили кубики друг на друга. Найдите высоту полученного параллелепипеда.
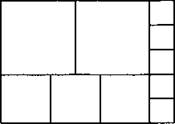
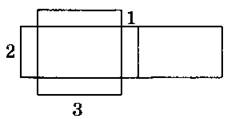
7. На рисунке изображена развертка прямоугольного параллелепипеда. Начертите еще несколько его разверток.
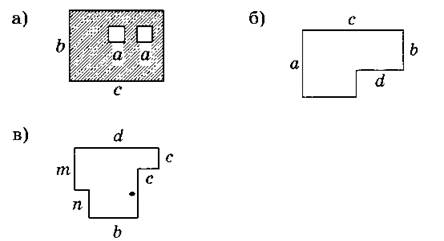
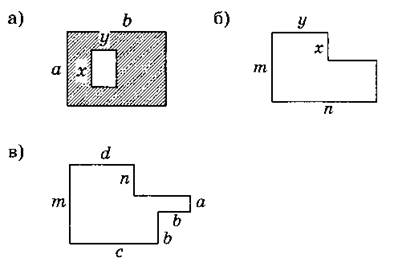
8. Запишите выражение для вычисления площади фигуры:
Вариант 2
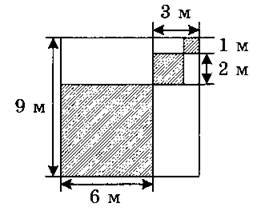
1. Найдите площадь окрашенной части квадрата.
2. Пусть одна тетрадная клетка изображает участок площадью 50 м2. Изобразите прямоугольный участок площадью 10а.
3. Сколько квадратов изображено на рисунке?
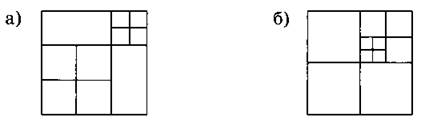
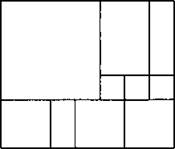
4. Прямоугольник разрезали на квадраты (см. рис.). Сторона наименьшего квадрата равна 6 см. Найдите периметр и площадь прямоугольника.
5. а) Сколько квадратов, равных данному, надо взять, чтобы сложить из них квадрат со стороной в 5 раз больше, чем сторона данного квадрата?
б) Сколько кубов, равных данному, надо взять, чтобы сложить из них куб, со стороной в 6 раз больше, чем сторона данного куба?
6. Прямоугольный параллелепипед с размерами 3 м, 5 м, 7 м разрезали на кубические дециметры и поставили кубики друг на друга. Найдите высоту полученного параллелепипеда.
7. На рисунке изображена развертка прямоугольного параллелепипеда. Начертите еще несколько его разверток.
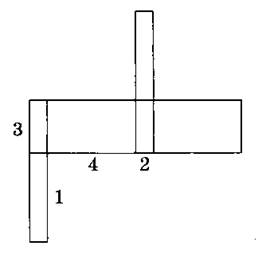
8. Запишите выражение для вычисления площади фигуры: