Движение тела под действием силы тяжести. Свободное падение - Основы динамики - МЕХАНИКА

Свободным падением называется движение тела, обусловленное притяжением Земли, при отсутствии начальной скорости и сопротивления среды.

Свободно падающее тело движется поступательно, прямолинейно и равноускоренно. Ускорение, с которым движется тело, называется ускорением свободного падения и обозначается буквой g. Формулы, описывающие движение свободно падающего тела, не содержат коэффициентов, зависящих от его формы и массы.

Другими словами, тела разной массы, которые мы уронили с одной высоты, достигнут поверхности земли за одно и то же время.

Кажущееся несовпадение последнего утверждения с нашим каждодневным опытом (например, все знают, что пушинка будет падать гораздо дольше, чем стальной шарик) связано с сопротивлением воздуха, т. е. с дополнительной силой, направленной вверх, следовательно, такое падение не является свободным. В этом можно убедиться на следующем опыте, впервые проведенном Ньютоном. Если взять пробирку длиной 1 м и опустить в нее одновременно свинцовый шарик, птичье перо и пробку, то все три предмета упадут на дно трубки в разное время: сначала шарик, затем пробка, последним — перо (рис. 1.23, а). Если теперь из пробирки откачать воздух и перевернуть ее вверх дном, можно увидеть, что все три предмета достигнут дна одновременно (рис. 1.23, б).

Впервые независимость ускорения свободного падения от массы тела опытным путем установил Галилей в конце XVI в. Для этого он одновременно ронял шары одинакового размера, но разные по весу (чугунный и деревянный), с Пизанской башни. Оба шара достигали земли практически одновременно.

Свободное падение тел является примером прямолинейного равноускоренного движения.

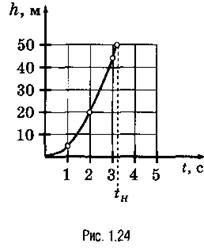
Для определения высоты тела над землей h при свободном падении можно воспользоваться уравнением (1.7) при следующих начальных условиях: h0 = 0, v0 = 0, а = g, что означает следующее: ось h направлена вниз, начало ее помещено в точку, в которой тело выронили (рис. 1.24):

График зависимости высоты от времени является параболой. Используя формулу (1.18) и выражение для скорости: v = vо + аt, (при v0 = 0, а = g), легко показать, что скорость связана с высотой соотношением:

Формулы (1.18) и (1.19) справедливы для любого прямолинейного движения с постоянным ускорением и нулевой начальной скоростью, а не только для свободного падения.

Тело, брошенное под углом к горизонту

Тело, брошенное под углом а к горизонту с начальной скоростью , будет двигаться по криволинейной траектории, в любой точке которой вектор скорости может быть разложен на две составляющие — горизонтальную и вертикальную (рис. 1.25).

Проекции этих векторов на оси координат, начало которых выбрано в точке бросания, равны:

При этом горизонтальная составляющая скорости не будет меняться с течением времени, т. к. ускорение свободного падения не имеет горизонтальной составляющей, а направлено вертикально вниз. Вертикальная составляющая скорости будет меняться по закону равнопеременного движения с ускорением a = g. Изменение координат тела согласно уравнению (1.7) имеет вид:

В уравнении (1.22) учтено, что ускорение силы тяжести направлено вниз (знак «-» перед вторым членом). Последняя пара уравнений позволяет найти уравнение траектории движения точки, которое представляет собой зависимость одной координаты от другой. Для этого из уравнений (1.21) и (1.22) исключим время и после простых преобразований получим:

Если ввести обозначения

последнее уравнение примет вид:

что является уравнением параболы с осью, параллельной вертикальной оси.

Таким образом, траектория тела, брошенного под углом к горизонту, представляет собой параболу. В вершине этой параболы вертикальная составляющая скорости равна нулю. В точке падения скорость тела равна по абсолютной величине скорости тела в точке бросания, а направление ее составляет тот же угол, что и в точке бросания (взятый с противоположным знаком). Это следует из симметрии параболы и имеет место в отсутствие сопротивления воздуха.

Траектория тела, брошенного горизонтально, также представляет собой параболу: тело будет двигаться по одной из ветвей параболы с вершиной в точке бросания (рис. 1.25).