Вектора и линейные операции над векторами - ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Цель: познакомить с векторами и операциями над ними.

Ход урока

I. Повторение. Беседа

1. Что называется перемещением толчки?

2. Каков смысл модуля перемещения?

3. Что называется телом отсчета?

4. Какими способами можно задать положение точки?

5. Что называют радиус-вектором?

II. Изучение нового материала

Известно, что некоторые физические величины полностью характеризуются числом, которое выражает отношение этой величины к единице измерения. Такие величины называют скалярными.

- Приведите пример таких величин. (Примерами могут служить масса, температура, плотность, энергия.)

Для характеристики других физических величин, например скорости, силы, недостаточно знать число, измеряющее их величину, необходимо знать и их направление. Такие величины называют векторными. В физике они играют большую роль. Вектор - направленный отрезок прямой.

У вектора есть начало и конец. Начало вектора называют так же точкой его приложения.

Если точка А является началом вектора а, то мы будем говорить, что вектор а приложен к точке А (рис. 4).

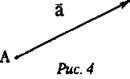
Число, выражающее длину направленного отрезка, называют модулем вектора, и обозначают той же буквой, что и сам вектор, но без стрелки сверху.

Если начало вектора совпадает с его концом, такой вектор называют нулевым.

Вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 5).

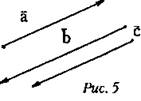
Два вектора называют равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление.

Из определения равенства векторов вытекает утверждение: каковы бы ни были вектор а и т. Р, существует единственный вектор с началом в т. Р, равный вектору а.

В физике принципиальное значение имеют линия, вдоль которой направлен вектор, и точка приложения вектора.

1. Сумма векторов.

Пусть даны два вектора а и b. Для нахождения их суммы нужно вектор в перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора а. Тогда вектор, проведенный из начала вектора а в конец перенесенного вектора b, и будет являться суммой а и b. с = а + b = b + а - правило треугольника.

Если два вектора коллинеарны и сонаправлены, то их сумма представляет собой вектор, направленный в ту же сторону и равный по модулю сумме модулей векторов слагаемых.

Если два вектора коллинеарны и направлены в противоположные стороны, то их сумма будет представлять собой вектор, модуль которого равен разности модулей векторов слагаемых, направленный в сторону того вектора-слагаемого, модуль которого больше.

Сумма векторов может быть найдена и по правилу параллелограмма (рис. 6).

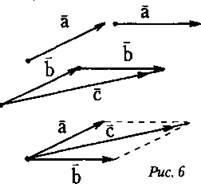
В этом случае параллельным переносом нужно совместить начала векторов а ив и построить на них параллелограмм. Тогда сумма а и b будет представлять собой диагональ этого параллелограмма.

2. Умножение вектора на скаляр.

Произведением вектора а на число k называют вектор b, коллинеарный вектору а, направленный в сторону, что и вектор а, если k > 0 и в направлен в противоположную сторону, если k< 0 b = ka, причем модуль b = lklа.

Если два вектора коллинеарны, то они отличаются только скалярным множителем.

Если k = -1, то b = -а. Вектор -а имеет модуль равный модулю вектора а, но направлен в противоположную сторону.

Два вектора, противоположно направленные и имеющие равные длины, называются противоположными. А и -а представляют собой противоположные векторы.

3. Разность векторов.

Вычитание векторов есть действие, обратное сложению.

Пусть необходимо из вектора b вычесть вектор а и тем самым найти их разность, т. е. h = b - a. Чтобы найти вектор разности, нужно по правилу параллелограмма (или треугольника) сложить вектор b с вектором, противоположным вектору а, т. е. с вектором -а (рис. 7).

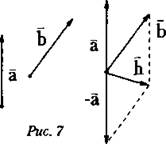
Разностью векторов b и а называют такой вектор h, который в сумме с вектором а дает вектор b. h = b - a и h + a = b по определению одно и то же.

III. Закрепление изученного

1. Какие величины называют скалярными, а какие - векторными?

2. Чем отличается векторная величина от скалярной?

3. Какие правила сложения векторов вы знаете?

4. Как производится сложение нескольких векторов?

5. Как определить разность двух векторов?

6. Какие вектора называются коллинеарными?

7. Как производится сложение и вычитание коллинеарных векторов?

IV. Решение задач

1. Начало вектора а задано координатами точки А (2;2), конец В (6;5). Построить вектор.

2. Эквивалентно замените силу F = 0,6 Н, приложенную в т. А, двумя силами, действующими на ту же точку вдоль той же прямой, но противоположные стороны. Меньшая из этих сил равна 1,1 Н. Каким должен быть модуль второй силы? (Ответ: 1,7 Н)

3. В одной точке приложены силы F₁ = 15 Н, F₂ = 24 Н, F₃ = 19 Н, F₄ = 20 Н. Определите их равнодействующую для случаев, когда

а) все данные силы действуют вдоль одной прямой в одну сторону.

б) все данные силы действуют вдоль одной прямой, первые две в одну сторону, а вторые две - в сторону, противоположную первым.

Домашнее задание

П. 5.