Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Ответы и указания

Аксиомы прямой. 3.1. 4. 6. 5.1, 4 или 6. 7. Могут. 8.190. 9.104. 10. 43. 12. АЕ пересекает прямую. 14. Аксиома полуплоскостей. 16. Нельзя. 18. Нет. 19. 24 или 210.

Отрезки. 3. Нет. 5. 4 см. 6. а/2. 7. 3,25 см. 8. 26:9. 9. 1 см или 4 см. 10.1,5 см или 3,5 см. 12. Точка С. 13. 5 или 11.14. 2 или 8.15.4 или 20.16. 49,5 см, 46,5 см, 43,5 см или 40,5 см. 17. 8/3.19. В любой точке отрезка между «средними» домами.

Углы. 1. 75°. 2. 90°. 4. 30° или 70°. 6. 110°. 8. 60°. 10. 130° или 50°. 12. 65°. 13. 6°. 14. а) 105°; б) 80°. 15.9 ч 12 мин. 17. « 22 сек. 18. 82,5° или 97,5°.

Ломаные, многоугольники. 1.0,1,2, 3,5,7.2.9 или 10. 3. а) 60; б) 12. 7. Могут. 8. Не обязательно. 9.170.10.11.11. Точка находится во внутренней области. 12. Может. 14. 8.

Выпуклые фигуры. 1. Фигура выпукла, если отрезок, соединяющий любые две точки фигуры, полностью принадлежит этой фигуре. 2. а) Да; б) да; в) нет. 3. Прямая разбивает плоскость на две выпуклые области.

Равнобедренный треугольник. 11. Нет, неверно.

Третий признак равенства треугольников. 4. Да.

Продолжение медианы на свою длину. 2. 1:2. 5. 55°. 6. Указание: продлите отрезок, соединяющий основания медиан, на свою длину.

Равенство прямоугольных треугольников. 1. Могут:

Теорема о большей стороне. 6. ZCBM> ZABM.

Неравенство треугольника. 3. 4, 5, 6. 4. 29. 12. 3, 4, 5, 6, 7. 13. Да. 22. Точка должна быть на пересечении диагоналей. 24. Указание: примените неравенство медианы. 25. Указание: попробуйте «вырезать» меньший треугольник из большего, делая разрезы по прямым линиям. 29. Может.

Параллельность. Сумма углов треугольника. 4. 40°. 7. 45°, 45°, 90° или 36°, 36°, 72°. 8. 50° или 70°. 9. 126°. 10. 360°. 12. 90° + а/2. 13. 2а. 14. 150°. 15. Верно. 16. Да. 18. 180°. 19. 180°. 21. 90°. 22.180°/7. 23. а) 45°; б) 72°; в) 36°; г) 54077. 24. 90°-а/2. 25. 90° + /3/2. 27. а) Да; б) да; в) нет. 28. Указание: подумайте, есть ли другие способы построения параллельной?

Расчет углов в равных треугольниках, дополнительные построения. 2. 45°. 6. Верно. 9. Может. 10. 45°. 11. 2. 12. 60°. 16. ВК.

Геометрические места точек. 2. а) Прямая является серединным перпендикуляром к АВ; б) прямая параллельна серединному перпендикуляру к АВ. 4. Одна. 6. Указание: рассуждайте от противного. 7. 2.

16. Луч ОК, где О — центр квадрата, К — середина АВ. 19. На двух прямых —биссектрисах двух пар вертикальных углов. 21. Одна. 22. Одна.

Знакомство с окружностью. 4. Нужные точки лежат на одной прямой с центром и с точкой А. 5. Точка лежит на перпендикуляре, опущенном из центра окружности на прямую. 13. 6. 25. а) Нет; б) да. 27. 80° или 160°. 28. 40°. 29. 3. 30. 45°.

Построения циркулем и линейкой. 12. Бесконечно много.

Знакомство с симметрией. 4. Можно. 8. Например, у = (х—I)². 13.1.14. 2.16. 2. 23. Не всегда.

Кратчайшие пути. 5.1. 6.1. 7. 0,5.

Отражения и зеркала. 8. 360° —2а. 9. 2а. 11.18.12. 1:3.13.11.

Центральная симметрия. 1. Можно. 8. Первый. 14. Верно. 18. Нет. 22. Всегда.

Параллелограммы. 6. 1:3 или 2:3.19. Верно.

Дополнительные построения, связанные с параллелограммом. 2. Одну. 5. 1:2. 7. а + 2Ь. 8. а + 2Ь. 9. Не могут. 10. 60° и 120°. 14. 9.15. Обязательно.

Трапеция. 1. Например, трапеза. 2. Обязательно. 6. Не существует. 9. Не более 4 решений. 11. Ь — а. 12. Нет. 13. 60°. 17. а + Ь. 18. а/2. 20. Ь —а. 21. Не могут. 22. Указание: разбейте треугольник на три трапеции. 23. Указание: разбейте данную трапецию на четыре трапеции.

Прямоугольник, ромб, квадрат. 16. 45°. 17. 45°. 18. 60°.

Медиана прямоугольного треугольника. 3. Четверть окружности. 8. 3:1. 9. СЬ —а)/2.10. (а + Ь)/2. И. (а + Ь)/2.

Средняя линия треугольника. 1. 3. 12. 60°. 13. Указание: проведите диагональ. 13. 0,5. 17. 1:3. 20. а/2. 21. с/4. 22. (Ь —а)/2. 26. 2:3. 28. 1:3. 36. Нет, не могут. 38. (а + Ь—с)/2.

Средняя линия трапеции. 4. Верно. 5. (а —Ь)/2. 6. 1:2. 7. 0,25. 8. На прямой, равноудаленной от данных прямых. 9. Указание: проведите диагональ. 11. |а + Ь — с — d\/2. 12. a) (p + q)/2; б) \р — q\/2. 13. 8. Указание: отметьте центр параллелограмма. 15. 19/32. 16. Указание: отметьте центры параллелограммов.

Медианы треугольника. 2. Можно. Указание: продлите отрезок, соединяющий основания медиан, на свою длину.. 4. 3:2. 5.2:1. 6.2:1. 8. 1:2.

Прямоугольный треугольник с углом 30°. 3. 30°. 4. 1:3. 5. 3/8. 6. 1:4. 7. 2а + Ь. 8. 0,25. 9. 15°. 10. 0,5.12. 60°. 13. 2:1.

Теорема Фалеса. 3.2/15.4. и ^4^. 5.1:2. 6. 5:7. 7.1:2.

8. 3,5. 14. 90°. 15. 0,5. 16. 3:1. 21. 3 : 7. 22. Точка движется по окружности вдвое меньшего радиуса. 35. Искомые точки лежат на окружности, центр которой находится в середине отрезка, соединяющего центры двух данных окружностей. 37. 0,25.

Касательные к окружности. 1. Указание: примените рассуждение от противного. 3. Центр движется по отрезку, параллельному полу. 9. Две. И. 90°. 12. 120°. 13. 1:2. 14. 75° и 105°. 15. 1,5. 17. 1. 19. 1,5. 20. (а + с-Ь)/2. 21.1. 22. 6. 26. |Ь-а|. 27. с. 28. 6. 31. 4.

Построение касательных. 15. Нет, не обязательно.

Касание окружностей. 1. Указание: проведите рассуждение от противного. 3. 2R. 5. 90°. 6. R/3. 7. 1:3. И. R + г. 17. 5 :3. 21. 135°.

Биссектрисы пересекаются в одной точке. 1. Верно. 3. 90° + + а/2. 4. Нет. 6. Можно. 7. а. 10. 0; 2 или 4. И. 90° - а/2.12. 2.13. 5. 15. 2,5.16. (а + Ь)/2.18. 1,5. 21. 80°.

Вписанные углы. 4. 30° или 150°. 15. а) 90°; б) 54°. 25.1. 26. а + Ь. 29. Верно.

Признаки вписанного четырехугольника. 4. 90°. 6. 45°. 7. 30° или 150°. 33. 70°. 35.135°. 39. 80° и 100°.

ГМТ с постоянным углом. 3. Да. 4. а) Нет; б) может. 7. Окружность, построенная как на диаметре на отрезке, соединяющем данную точку с центром данной окружности. Концы диаметра не входят в множество. 8. Объединение кругов с диаметрами ОА и ОВ без их пересечения. 9. Окружность, построенная как на диаметре на отрезке, соединяющем середины АС и BD без концов этого диаметра. 10. Все углы треугольника должны быть меньше 120°.

И. Одна. 12. а) Окружность, симметричная данной относительно прямой АВ. 14. Может, если угол равен 90°. 18. Не более 2 решений.

Обратный ход. 2.100°. 4. По окружности с центром в вершине угла. 5.110°. 6. 80°. 9. Одна. И. 30°.

Площади. 1. 144. 2. а) 3,5; б) 0,5. 4. 1:3. 5. а) 1/6; б) 1/3;

в) 5/9. 6. а) 7; б) 2,5. 10. 3 : 4. 13. Верно. 14. Одну. Указание: проведите медиану треугольника. 16. ch. 17. 3/8. 18. Нужные точки делят стороны квадрата в отношении 1 : 2. 19. 3. 25. 9. 26. 11. 27. Указание: расположите равные углы как вертикальные. 30. S³/(2a²b²). 31. (5 + VS)/2. 32. 7:2. 34. Всего существует 4 такие точки. 36. а) 1/12; б) 0,4. Указание: примените лемму о «бумажном самолетике». 37. а) 1/7; б) 11/60; в) 1/60. 38. 3,4.

39. 0,5. 41. 7 + 3V5. 42. 1/2. 44. 5/9. 45. 1/4. 46. 7. 47. 5. 52. 1/5. 53. 3/4. 55. 1/2. 56. 2rS²/abc.

Применение площадей. 2. аЪ/с. 3.2,5.4.3,4. 5. ab/(a + b). 6.4,4. 7. 0,2.12. Верно. 14. 20:27.15. Указание: а) воспользуйтесь леммой «о крыльях самолетика»; б) проведите рассуждение от противного. 18. 4:7. 21. Верно. 25. 60/47. 26.1,5. 30. 5,9. 31. 1:6.

Теорема Пифагора. 2. Неверно. 4. 7 метров. 5. 2,5. 7. 6. 8. 13 метров. 10.11:21. И. 25/8.12.5.13.1:3.14. 3:5.15. VMh ~ 4,6 км. 17. 4.18. pq. 19. 4,8. 20. Vab. 26. 4. 27. Vab. 28. 1:3. 32. 4. 33.13. 34. 20. 35. 5,25. 36. 24. 40. c + h. 42. 4 м 95 см. 43. 1:7. 44. \/б- л/2. 45. 2. 46.1,6. 47.1,44 или 36. Указание: воспользуйтесь задачей 17. 48. 0,2. 49. 0,2. 50. 0,4. 51. 0,5. 52. а) 1/6; б) 1/4; в) 0,16; г) 2/9. 53. а + Ь — с. 54. 0,2. 55. Rr/(R + r). 56. 1 (для симметричного слу

чая) или

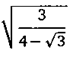
(для несимметричного случая).

Учебно-методическое издание Волчкевич Максим Анатольевич

УРОКИ ГЕОМЕТРИИ В ЗАДАЧАХ. 7—8 КЛАССЫ

Подписано к печати 01.02.2016 г. Гарнитура ITC Charter. Формат 60 х 90/16. Печать офсетная. Объем 13 печ. л. Тираж 3000 экз. Заказ № 2494.

Издательство Московского центра непрерывного математического образования 119002, Москва, Большой Власьевский пер., 11. Тел. (499) 241-08-04

Отпечатано в ОАО «Тверской полиграфический комбинат» 170024, г. Тверь, пр-т Ленина, 5 Тел. (4822) 44-42-15, (495) 748-04-67. Тел./факс (4822) 55-42-15

Книги издательства МЦНМО можно приобрести в магазине «Математическая книга», Москва, Большой Власьевский пер., д. 11. Тел. (495) 745-80-31. E-mail: biblioQmccme.ru

ДЛЯ ЗАМЕТОК

Книга обобщает авторский опыт преподавания геометрии в нескольких московских школах. В ней много рисунков — это сильно экономит время на уроках. Перед каждым параграфом дается справочный материал — формулировки основных теорем и определения.

Материал каждой темы строится по классическому принципу: от простого к сложному. Первые задачи доступны каждому школьнику, последние достигают уровня серьезных математических олимпиад.

Около половины всех задач авторские. Подборка к каждой теме выстроена так, чтобы показать содержащийся в ней метод со всех сторон.

Данная книга составлена именно для работы на уроках, поэтому решений в ней нет, только ответы.