Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Площади
Площадью фигуры называют число, показывающее, сколько раз единичный квадрат и его части укладываются в данной фигуре. Для площадей справедливы свойства (или аксиомы), аналогичные аксиомам отрезков2.
Аксиомы ПЛОЩАДИ
ъ
а
S = ab
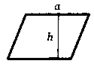
S = ah
а
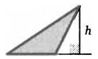
S = ah/2 а
Ь
S=(a + b)h/2
1. Площадь любой фигуры является неотрицательным числом.
2. Равные фигуры имеют равные площади.
3. Если фигура составлена из двух неперекры-вающихся частей, то ее площадь равна сумме площадей этих частей.
4. Площадь квадрата со стороной, равной единице измерения, равна 1.
Теорема о площади прямоугольника. Площадь прямоугольника равна произведению двух его соседних сторон.
Теорема о площади параллелограмма. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Теорема о площади треугольника. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Теорема о площади трапеции. Площадь трапеции равна произведению ее высоты на среднюю линию.
1. В одном футе 12 дюймов. Сколько квадратных дюймов в квадратном футе?
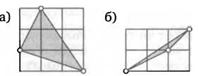
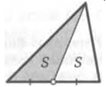
2. Сколько клеток составляет площадь закрашенного треугольника на рисунках?![]()
3. (Свойство медианы треугольника.) Докажите, что медиана делит площадь треугольника пополам.
4. В каком отношении делит площадь треугольника его средняя линия?
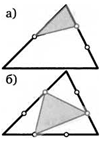
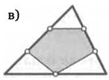
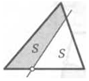
5. Площадь треугольника равна 1. Каждая его сторона отмеченными точками делится на равные части. Найдите площади закрашенных фигур на рисунках.
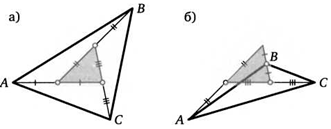
6. Площади закрашенных треугольников равны 1. Их стороны продолжили так, как показано на рисунках. Найдите площадь треугольника ЛВС.
7. Докажите, что медианы треугольника разбивают его на шесть равновеликих частей.
8. (Лемма о «крыльях бабочки».) Диагонали трапеции делят ее на четыре треугольника. Докажите, что площади двух треугольников, прилегающих к ее боковым сторонам, равны. Сформулируйте обратное утверждение и докажите его.
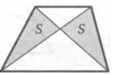
9. Отмеченные на рисунке точки — середины сторон трапеции. Докажите, что площади закрашенных фигур равны.
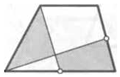
10. Вершину трапеции соединили с серединой другой боковой стороны. Известно, что полученный отрезок делит ее площадь в отношении 2:5. Найдите отношение оснований трапеции.
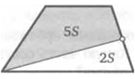
11. Отрезок, соединяющий середины противоположных сторон четырехугольника, делит его площадь пополам. Докажите, что две стороны четырехугольника параллельны.
12. В пятиугольнике ABCDE стороны ВС и CD параллельны соответственно диагоналям AD и BE. Докажите, что треугольники АВС и CDE равновелики.
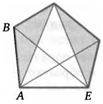
13. В пятиугольнике ABCDE стороны АВ, ВС и CD параллельны диагоналям СЕ, AD и BE соответственно. Верно ли, что треугольники АВЕ и CDE равновелики?
14. Через данную точку на стороне треугольника проведите прямую так, чтобы она делила его площадь пополам. Сколько таких прямых можно провести?
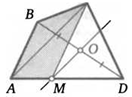
15. Через точку О — середину диагонали BD четырехугольника ABCD параллельно его диагонали АС провели прямую. Она пересекла сторону AD в точке М. Докажите, что отрезок СМ делит площадь четырехугольника пополам.
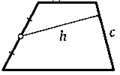
16. Боковая сторона трапеции равна с, а расстояние до нее от середины другой боковой стороны h. Найдите площадь трапеции.
Задачи с параллелограммами
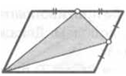
17. Вершина параллелограмма и середины противоположных от нее сторон образуют треугольник. Какую часть составляет его площадь от площади всего параллелограмма?
18. Как разрезать квадрат по двум прямым, проходящим через его вершину, на три равновеликие части?
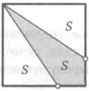
19. Точку внутри параллелограмма соединили со всеми его вершинами. Полученные отрезки разбили его на четыре треугольника. Площади трех из них, взятые по порядку, равны 2, 4 и 5. Найдите площадь четвертого.
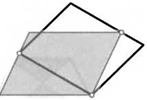
20. Два параллелограмма расположены так, как показано на рисунке. Докажите, что их площади равны.
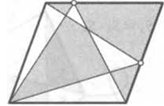
21. Две точки на сторонах параллелограмма соединили с тремя его вершинами так, как это показано на рисунке. Докажите, что площадь одной из закрашенных на рисунке частей равна сумме площадей других.
22. Параллелограмм разрезали на четыре меньших параллелограмма. Два из них, закрашенные на рисунке, имеют равные площади. Докажите, что их общая вершина лежит на диагонали большого параллелограмма.
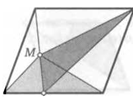
23. Внутри параллелограмма ABCD взяли произвольную точку М. Прямая ВЫ пересекает AD в точке Е. Докажите, что площади треугольников AMD и СМЕ равны.
Отношение площадей треугольников с равным углом
24. (Лемма о «воздушном змее».) Диагонали разбивают четырехугольник на четыре треугольника. Докажите, что произведение площадей двух треугольников, прилегающих к его противоположным сторонам, равно произведению площадей других двух треугольников.
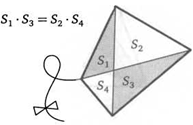
25. Диагонали трапеции разбивают ее на четыре треугольника. Площади двух из них, прилегающих к основаниям, равны 1 и 4. Найдите площадь трапеции.
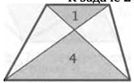
26. В параллелограмме провели диагональ, а через не лежащую на ней вершину —прямую. Они разбили параллелограмм на три треугольника и четырехугольник. Площади двух треугольников на рисунке равны 1 и 3. Найдите площадь четырехугольника.
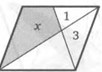
27. (Теорема об отношении площадей треугольников с равным углом.) Два треугольника имеют по равному углу. Докажите, что их площади относятся как произведения сторон, заключающих этот угол.
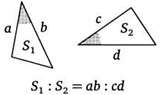
28. Докажите утверждение, аналогичное предыдущей теореме, но для случая, когда углы дополняют друг друга до 180°.
29. На сторонах треугольника построили квадраты. Докажите, что закрашенные треугольники на рисунке равновелики.
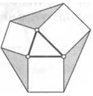
30. Из вершины параллелограмма на две его противоположные стороны опустили высоты. Найдите площадь треугольника, образованного этими высотами, если стороны параллелограмма равны а и Ь, а его площадь равна S.
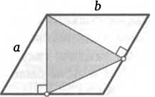
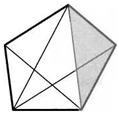
*31. Каждая диагональ пятиугольника отсекает от него треугольник единичной площади. Найдите площадь пятиугольника.
Расчет частей треугольника
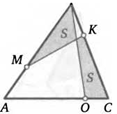
32. На сторонах АВ и ВС треугольника АВС взяли точки М и К так, что AM: МВ = ВК : КС = 1:2. Вершину В соединили отрезком с такой точкой О на стороне АС, чтобы площади закрашенных на рисунке треугольника и четырехугольника были равны. Найдите АО: ОС.
В
33. Точки М и К на сторонах треугольника соединили с противоположными вершинами. Оказалось, что закрашенные на рисунке треугольник и четырехугольник равновелики. Докажите, что точки М и К делят стороны в одинаковом отношении.
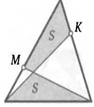
34. В треугольнике АВС найдите такую точку М, чтобы площади треугольников ABM, ВСМ и ACM были равны. Существуют ли такие точки вне треугольника?
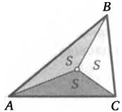
35. («Лемма о бумажном самолетике».) На стороне АС треугольника АВС взяли произвольную точку М. На отрезке ВМ взяли произвольную точку К. Докажите, что площади треугольников АВК и СВК относятся как AM : МС.
В
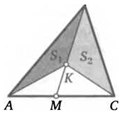
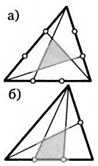
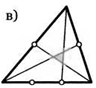
36. Каждую сторону треугольника разделили на равные части. Какую часть его площади составляют закрашенные треугольники на рисунках?
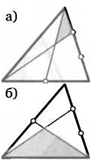
37. Каждую сторону треугольника разделили на равные части. Какую часть его площади составляют закрашенные фигуры на рисунках?
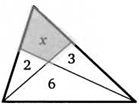
38. Две прямые делят треугольник на три треугольника и один четырехугольник. На рисунке цифрами обозначены площади треугольников. Найдите площадь четырехугольника.
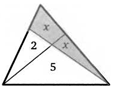
39. Две прямые делят треугольник на три треугольника и четырехугольник. Площади двух треугольников на рисунке равны 2 и 5. Найдите площадь четырехугольника, если он равновелик третьему треугольнику.
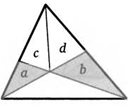
40. Буквы на рисунке обозначают площади треугольников. Докажите, что, если а = Ъ, то с = d.
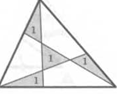
*41. Через каждую вершину треугольника провели прямую. Эти прямые разбивают треугольник на четыре меньших треугольника и три четырехугольника. Площади каждого из указанных треугольников равны 1. Докажите, что площади всех четырехугольников равны и найдите площадь исходного треугольника.
Группировка площадей
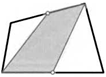
42. Середины двух противоположных сторон четырехугольника соединили с двумя его вершинами так, как это показано на рисунке. Какую часть от площади исходного четырехугольника составляет закрашенная фигура?
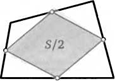
43. В четырехугольнике отметили середины всех сторон. Докажите, что площадь параллелограмма с вершинами в этих точках составляет половину площади исходного четырехугольника.
44. Каждую сторону выпуклого четырехугольника разделили на три равные части. Соответствующие точки соединили так, как это показано на рисунке. Какую часть исходного четырехугольника составляет закрашенная фигура?
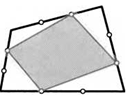
45. Середины диагоналей выпуклого четырехугольника соединили с двумя его вершинами так, как это показано на рисунке. Какую часть от площади четырехугольника составляет закрашенная фигура?
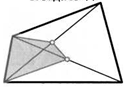
46. Параллелограмм разбили на девять меньших параллелограммов так, как это показано на рисунке. Найдите площадь четырехугольника ABCD, если площадь центрального параллелограмма равна 1, а площадь исходного —13.
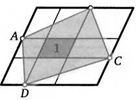
47. Площадь закрашенного четырехугольника равна 1. Все его стороны продолжили на свою длину так, как это показано на рисунке. Найдите площадь получившегося большого четырехугольника.
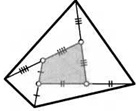
48. Вершины четырехугольника соединили с серединами его сторон так, как показано на рисунке. Докажите, что площадь закрашенного четырехугольника равна сумме площадей закрашенных треугольников.
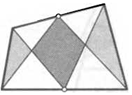
49. Середину стороны четырехугольника соединили с противоположными вершинами. Оказалось, что полученный треугольник составляет половину его площади. Докажите, что у четырехугольника две стороны параллельны.
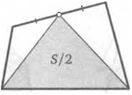
50. Две противоположные стороны выпуклого четырехугольника разделили на три равные части. Соответствующие точки деления соединили так, как показано на рисунке. Докажите, что между получившимися отрезками находится ровно треть площади исходного четырехугольника.
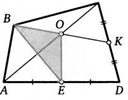
51. Точки Е и К — середины сторон AD и CD четырехугольника ABCD. Отрезок ВК пересекает диагональ АС в точке О. Докажите, что площадь треугольника ОВЕ в два раза меньше площади треугольника АВС.
С
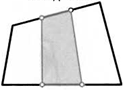
52. Вершины параллелограмма соединили с серединами его сторон так, как показано на рисунке. Какую часть площади параллелограмма составляет закрашенная фигура в центре?
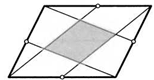
53. Из медиан треугольника составили новый треугольник. Как относятся их площади?
54. Противоположные стороны шестиугольника ABCDEF попарно параллельны. Докажите, что треугольники АСЕ и BDF равновелики.
Е D
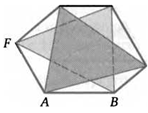
55. Площадь треугольника равна 1. Из середины каждой стороны треугольника опустили перпендикуляры на другие его стороны. Найдите площадь образованного ими шестиугольника.
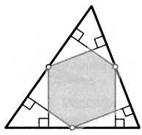
*56. Окружность с радиусом г вписана в треугольник. Она касается его сторон в точках М, Е, К. Найдите площадь треугольника МЕК, если площадь исходного треугольника равна S, а его стороны равны а, Ъ, с.
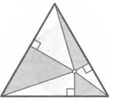
*57. Внутри равностороннего треугольника взяли точку. Ее соединили со всеми его вершинами, а также опустили перпендикуляры на все стороны. Получившиеся при этом шесть треугольников покрасили в черный и белый цвета так, как это показано на рисунке. Докажите, что сумма площадей черных треугольников равна сумме площадей белых.
*58. Середины диагоналей выпуклого четырехугольника соединили с точкой пересечения продолжений двух его противоположных сторон. Докажите, что площадь получившегося треугольника равна 1/4 площади четырехугольника.