Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Биссектрисы пересекаются в одной точке
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Окружность называется вневписанной в треугольник, если она касается одной его стороны и продолжений двух других. Всего у треугольника существуют три вневписанные окружности.
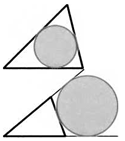
вписанная окружность вневписанная окружность
Теорема о вписанной окружности треугольника. В любой треугольник можно вписать единственную окружность. Центр вписанной окружности лежит на пересечении биссектрис всех углов треугольника.
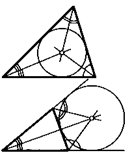
Теорема о вневписанной окружности треугольника. В любом треугольнике существует единственная вневписанная окружность, касающаяся его данной стороны. Центр вневписанной окружности лежит на пересечении биссектрис двух внешних и одного внутреннего угла треугольника.
Теорема об описанном четырехугольнике. Для того чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы сумма длин одной пары его противоположных сторон равнялась сумме длин другой пары.
1. В многоугольник можно вписать окружность. Докажите, что биссектрисы всех его углов пересекаются в одной точке. Верно ли обратное?
2. Докажите терему о вписанной окружности треугольника.
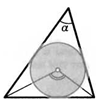
3. Окружность вписана в треугольник. Найдите угол, под которым из ее центра видно его основание, если противоположный основанию угол треугольника равен а.
4. Может ли центр вписанной окружности треугольника лежать на его средней линии?
5. Через центр вписанной окружности треугольника провели прямую, параллельную одной его стороне. Докажите, что эта прямая отсекает от данного треугольника меньший треугольник, периметр которого равен сумме двух сторон данного треугольника.
6. Можно ли произвольный треугольник разрезать на шесть равнобедренных треугольников?
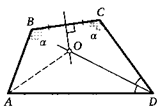
7. В четырехугольнике ABCD углы В и С равны а. Биссектриса угла D пересекает серединный перпендикуляр к стороне ВС в точке О. Найдите ZAOD.
8. В выпуклом шестиугольнике ABCDEF, все углы которого тупые, ZA = ZB, ZC = ZD, ZE = ZF. Докажите, что серединные перпендикуляры к его сторонам АВ, CD, EF пересекаются в одной точке.
9. Докажите теорему о вневписанной окружности треугольника.
10. Сколько может быть окружностей, касающихся трех данных различных прямых?
11. Точка О — центр вневписанной окружности треугольника АВС, касающейся стороны ВС. Найдите Z.BOC, если ABAC = а.
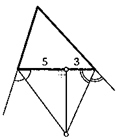
12. Провели биссектрисы двух внешних углов треугольника. Из точки их пересечения на его сторону опустили перпендикуляр. Он делит ее на отрезки с длинами 3 и 5. Найдите разность двух других сторон треугольника.
13. Биссектрисы трех углов четырехугольника пересекаются в одной точке. Длины трех его сторон в указанном порядке равны 3, 4, 6. Найдите четвертую сторону.
14. Окружность высекает на всех сторонах четырехугольника равные хорды. Докажите, что биссектрисы всех его углов пересекаются в одной точке.
15. Основания трапеции равны 3 и 5, а ее боковые стороны равны 1 и 2. Каждая из двух окружностей касается трех сторон трапеции. Найдите расстояние между их центрами.
3
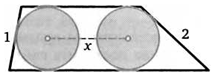
5
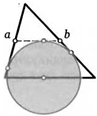
16. Окружность с центром на основании треугольника касается его боковых сторон и средней линии. Найдите основание, если боковые стороны треугольника равны а и Ъ.
17. Биссектрисы соседних углов четырехугольника пересекаются в середине его стороны. Докажите, что либо у этого четырехугольника равны два угла, либо две стороны параллельны.
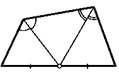
18. От угла равностороннего треугольника со стороной 1 отрезали меньший треугольник так, что биссектриса его внешнего угла делит пополам сторону исходного треугольника, противоположную данному углу. Найдите периметр отрезанного треугольника.
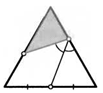
19. От квадрата со стороной 1 отрезали треугольник с периметром 2 так, как показано на рисунке. Докажите, что отмеченный на нем угол всегда равен 45°.
С
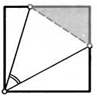
20. Стороны угла пересекаются за краем бесконечного листа бумаги (полуплоскости). Как построить след его биссектрисы на листе, не выходя за край?
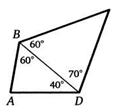
21. Дан четырехугольник ABCD, в котором ZABD = ZCBD = 60°, ZADB = 40°, a ZBDC = 70°. Найдите угол между его диагоналями.
22. Восстановите треугольник по центрам трех его вневписан-ных окружностей.
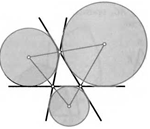
23. Постройте треугольник по центрам его вписанной и двух вневписанных окружностей.
24. На сторонах треугольника выбраны три точки так, что отмеченные на рисунке углы равны. Докажите, что данные точки — основания высот треугольника.
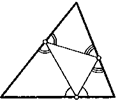
25. Основания высот данного треугольника образуют прямоугольный треугольник. Докажите, что один из углов данного треугольника равен 45°.
26. Один из углов треугольника равен 120°. Докажите, что треугольник, образованный основаниями его биссектрис, прямоугольный.
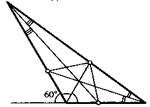
27. На сторонах АВ и ВС треугольника АВС взяли соответственно точки М и К так, что AM = АС = СК. Отрезки АК и СМ пересеклись в точке Е. Докажите, что перпендикуляр, опущенный из точки Е на сторону АС, проходит через центр вписанной в треугольник окружности.
В
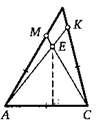
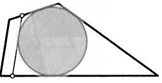
28. (Признак описанного четырехугольника.) Суммы противоположных сторон выпуклого четырехугольника равны. Докажите, что в него можно вписать окружность. (Для доказательства воспользуйтесь приведенным чертежом.)
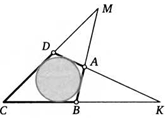
29. Продолжения сторон АВ и CD выпуклого четырехугольника ABCD пересекаются в точке М, а продолжения сторон AD и ВС — в точке К. Докажите, что если выполняется условие ВК + ВМ = = DK + DM, то в этот четырехугольник можно вписать окружность.
30. Про выпуклый пятиугольник ABCDE известно, что АВ + + CD = ВС + DE, причем его тупые углы А и Е равны. Докажите, что биссектрисы трех углов этого пятиугольника пересекаются в одной точке.
*31. У выпуклого пятиугольника есть три равных острых угла и две пары равных сторон, расположенных так, как это показано на рисунке. Докажите, что в данный пятиугольник можно вписать окружность.
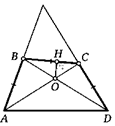
*32. Про четырехугольник ABCD известно, что АВ = ВС = CD, его диагонали пересекаются в точке О, а продолжения сторон АВ и CD — в точке К. Из точки О на сторону ВС опущен перпендикуляр ОН. Докажите, что ВК + ВН = СК 4- СН.
К
33. Противоположные стороны шестиугольника попарно параллельны, а три его диагонали, соединяющие противолежащие вершины, равны. Докажите, что данный шестиугольник можно вписать в окружность.