Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Прямоугольный треугольник с углом 30
1. (Свойство прямоугольного треугольника с углом 30°.) Докажите, что катет прямоугольного треугольника, лежащий против угла 30°, в два раза меньше его гипотенузы.
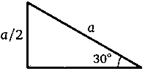
2. (Признак прямоугольного треугольника с углом 30°.) В прямоугольном треугольнике один катет в два раза короче гипотенузы. Докажите, что против него лежит угол 30°.
3. Одна сторона треугольника в два раза длиннее другой, а угол между ними равен 60°. Найдите меньший из углов треугольника.
4. Острый угол прямоугольного треугольника равен 30°. На его гипотенузу опустили высоту. В каком отношении она ее делит?
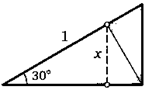
5. Острый угол прямоугольного треугольника равен 30°, а его гипотенуза равна 1. Найдите длину отмеченного пунктиром на рисунке отрезка.
6. Острый угол прямоугольного треугольника равен 30°. К его гипотенузе провели серединный перпендикуляр. В каком отношении он делит больший катет треугольника?
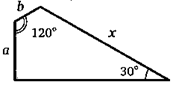
7. Выразите сторону четырехугольника, обозначенную буквой х на рисунке, через его стороны а и Ь.
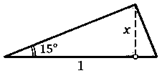
8. Гипотенуза прямоугольного треугольника равна 1, а один из его углов равен 15°. Найдите высоту треугольника, опущенную на гипотенузу.
9. Квадратный лист бумаги сложили вдвое, а затем перегнули так, показано на рисунке. Чему равен отмеченный угол?

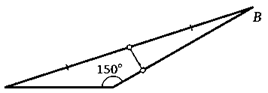
10. Угол С треугольника АВС равен 150°. Из середины стороны АВ на сторону ВС опустили перпендикуляр. Найдите длину этого перпендикуляра, если АС = 1.
А 1 С
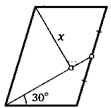
11. Вершину параллелограмма соединили с серединой его противоположной стороны. Полученный отрезок образует с другой его стороной угол 30°. Докажите, что отмеченный на рисунке перпендикуляр равен одной из сторон параллелограмма.
12. В треугольнике медиана равна высоте, проведенной к другой его стороне. Найдите угол между ними.
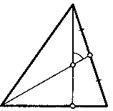
13. Найдите отношение двух сторон треугольника, если его медиана, выходящая из той же вершины, образует с этими сторонами углы 30° и 90°.
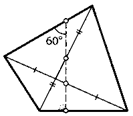
14. Прямая, проходящая через середины диагоналей четырехугольника, перпендикулярна одной его стороне, а с противоположной стороной образует угол 60°. Докажите, что расстояние между серединами диагоналей равно четверти одной из сторон четырехугольника.