Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Знакомство с симметрией
Осевая симметрия
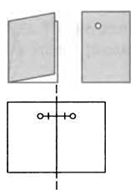
Сложите обычный лист бумаги по прямой линии и проткните его иголкой. Если теперь снова разложить его на плоскость, точки прокола будут находиться по разные стороны от линии сгиба бумаги и на равных от нее расстояниях. Такие точки называют симметричными относительно прямой.
Таким образом, при симметрии относительно прямой для каждой точки А на плоскости находят такую точку Al9 что данная прямая будет серединным перпендикуляром к отрезку АА1. Эту прямую называют осью симметрии, а саму симметрию осевой. Если точка лежит на оси, считается, что она совпадет с симметричной ей точкой. Симметрия относительно прямой I обозначается так: St.
Говорят, что фигура имеет ось симметрии, если при симметрии относительно этой оси фигура переходит сама в себя.
О-h
Л
I
+
Ai
осевая симметрия S/
3. Обрывок листа бумаги не имеет ни одного ровного края. Как без циркуля и линейки получить на нем прямой угол? А угол 22,5°?
4. Можно ли так сложить обычный лист бумаги, чтобы одним прямолинейным разрезом сделать в нем квадратную дыру?
5. Покажите, что окружность симметрична относительно любой прямой, проходящей через ее центр.
6. Докажите, что равнобедренный треугольник имеет ось симметрии.
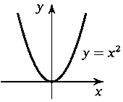
7. На рисунке показан график функции, заданной уравнением у = х3. Докажите, что он имеет ось симметрии.
8. Напишите уравнение какой-нибудь числовой функции, график которой симметричен относительно вертикальной прямой х — \.
9. Докажите, что осевая симметрия сохраняет расстояния между точками на плоскости4.
10. Докажите, что при осевой симметрии отрезок переходит в отрезок, а прямая линия — в прямую.
11. Докажите, что при осевой симметрии угол переходит в равный ему угол.
12. Докажите, что при осевой симметрии окружность переходит в окружность.
13. Сколько осей симметрии имеет угол, отличный от развернутого?
14. Сколько существует симметрий, переводящих данный отрезок в себя?
15. Нарисуйте четырехугольник, имеющий: а) только одну ось симметрии; б) ровно две оси симметрии.
16. Две прямые пересекаются под острым углом. Сколько осей симметрии имеет образованная ими фигура?
17. В окружности провели две параллельные хорды АВ и CD, Докажите, что АС = BD,
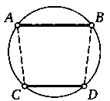
18. Две прямые пересекают окружность, центр которой лежит на биссектрисе угла между ними. Докажите, что эти прямые высекают на окружности равные хорды.
19. Через точку внутри окружности провели две равные хорды. Докажите, что они симметричны относительно одного из ее диаметров.
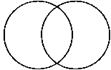
20. Докажите, что фигура, состоящая из двух равных окружностей, обладает двумя осями симметрии.
21. На круглом торте нарисован дракон, глаз которого не находится в центре круга. Разрежьте данный торт на две части и переложите их так, чтобы они снова образовали круглый торт, а глаз дракона оказался бы точно в его центре.

22. Точки А и В лежат по одну сторону от прямой. Постройте на этой прямой такую точку М, чтобы отрезки AM и ВЫ образовывали с данной прямой равные углы.
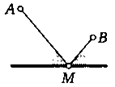
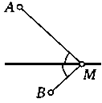
23. Решите задачу, аналогичную предыдущей, если точки А и В лежат по разные стороны от прямой. Всегда ли это возможно?
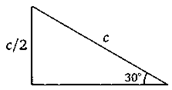
24. (Теорема.) Острый угол прямоугольного треугольника равен 30°. Докажите, что лежащий против него катет в два раза меньше гипотенузы.
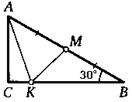
25. Точка М — середина гипотенузы АВ прямоугольного треугольника АВС, угол В которого равен 30°. На его катете ВС выбирают такую точку К, что АК 4- КМ = ВС. Докажите, что МК _L АВ.
26. На гипотенузе АВ и катете ВС прямоугольного равнобедренного треугольника АВС соответственно взяли произвольные точки М и К. Докажите, что АК 4- КМ > АВ.
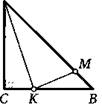
27. Из точки, лежащей на диаметре полукруга, под равными к нему углами провели два отрезка так, как показано на рисунке. Докажите, что сумма этих отрезков не больше диаметра полукруга.
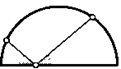
28. Внутри острого угла с вершиной О взяли произвольную точку А. Ее отразили относительно сторон угла и получили точки Аг и А2. Докажите, что угол АгОА2 не зависит от выбора точки.
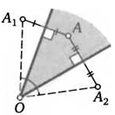
29. В четырехугольнике ABCD угол BAD прямой. Докажите, что ВС 4- CD 4- BD > 2 • АС.
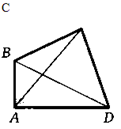
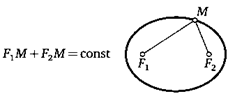
30. Эллипсом называют множество всех точек на плоскости, сумма расстояний от которых до двух данных точек (называемых его фокусами) постоянна. Внешне эллипс похож на овал или вытянутую окружность. Докажите, что эллипс имеет две оси симметрии, причем эти оси перпендикулярны друг другу.
31. Постройте треугольник, если даны одна его вершина и три прямые, на которых лежат его биссектрисы.
32. Постройте треугольник по длинам двух его сторон и разности лежащих против них углов.
33. Постройте треугольник по двум его углам и разности противолежащих им сторон.
34. Биссектриса АЕ равнобедренного треугольника АВС пересекает биссектрису его угла В в точке О. На боковой стороне АВ взяли точку М так, что AM = АС. Прямая МО пересекает основание АС в точке К. Докажите, что АК = ЕС.
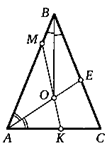
*35. На листе бумаги нарисован треугольник. Сложите этот лист так, чтобы одним прямым разрезом получить в нем дыру в виде данного треугольника.
