Математические олимпиады по лигам. 5–9 классы - Андрей Николаевич Павлов 2007
Олимпиады по лигам (5-6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон
Суперлига
1 тур
1. В пруд пустили 30 щук, которые постепенно поедали друг друга. Щука считается сытой, если она съела 3 щук (сытых или голодных). Каково наибольшее число щук, которые могут насытиться?
2. В бочке 10 литров бензина. Как отлить из нее 6 литров с помощью девятилитрового ведра и пятилитрового бидона?
3. Отец старше сына в 4 раза, а сумма их возрастов составляет 50 лет. Через сколько лет отец станет втрое старше сына?
4. Расставьте в записи 4 ? 12 + 18:6 + 3 скобки так, чтобы получилось: а) число 50; б) наименьшее возможное число; в) наибольшее возможное число.
5. При сложении двух целых чисел ученик по ошибке поставил во втором слагаемом лишний нуль на конце и получил в сумме 6641 вместо 2411. Определите слагаемые.
6. При делении одного числа на другое получилось в частном 28 и в остатке 84. Как изменится частное и как изменится остаток, если делимое и делитель уменьшить в 7 раз?
2 тур
1. Куб со стороной 1 м распилили на кубики со стороной 1 см. Получившиеся кубики выложили вряд. Чему равна длина ряда?
2. Применяя знаки арифметических действий и, возможно, скобки, запишите восемью двойками число 200 (разрешено использовать такие числа, как 22, 222, 2222 и т. д.).
3. Во сколько раз увеличится трехзначное число, если справа к нему приписать такое же число? Ответ подтвердите двумя примерами.
4. Докажите, что из любых трех целых чисел можно найти два, сумма которых делится на 2.
5. Сошлись два пастуха, Иван и Петр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Петр ему отвечает: «Нет! Лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
6. На прямоугольном торте лежит круглая шоколадка, причем отнюдь не посередке. Как разрезать торт на две равные части так, чтобы и шоколадка тоже разделилась ровно пополам?
3 тур
1. В коробке лежат 4 цветных карандаша и 10 простых. Берут из этой коробки наугад несколько карандашей. Какое наименьшее число карандашей надо взять из коробки, чтобы среди них с гарантией оказалось не менее: а) двух цветных; б) трех простых?
2. Поблизости один от другого расположены два населенных пункта, А и В. Все жители А говорят только правду, а жители В всегда лгут. Жители А и В посещают друг друга. Ты находишься в каком-то из этих пунктов. Какой вопрос (только один) ты можешь задать первому встретившемуся тебе в этом пункте человеку, чтобы по ответу на этот вопрос ты мог установить, А это или В?
3. Два мальчика играли в шашки. Положение первого игрока стало ухудшаться. Пока он обдумывал очередной ход, второй игрок рассматривал доску, на которой стояли шашки. Оказалось, что пустых клеток на доске было втрое больше, чем занятых шашками, и что у него на две шашки больше, чем у первого игрока. Сколько шашек у каждого игрока было в это время на доске?
4. Школьники ехали на автомашине из деревни в город. Когда они проехали 3/4 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути школьники проделали пешком, затратив на это времени в четыре раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали школьники на автомашине, чем шли пешком?
5. Дано трехзначное число ABB, произведение цифр которого — двузначное число AC, произведение цифр этого числа равно С (здесь цифры в записи числа заменены буквами; одинаковым буквам соответствуют одинаковые цифры, разным — разные). Определите исходное число.
6. Ребята принесли из леса по полной корзинке грибов. Всего было собрано 289 грибов, причем в каждой корзинке их оказалось одинаковое количество. Сколько было ребят?
4 тур
1. Упростите выражение (2 + х — 1 + Зх): (7х + 6 — 3х — 5).
2. Восстановите недостающие цифры:
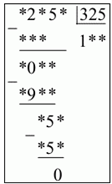
3. На колхозном рынке продаются два арбуза разных размеров. Первый в диаметре 40 см, а второй — 80 см. Первый арбуз стоит 30 р., второй арбуз стоит 180 р. Какой из арбузов выгоднее купить и почему?
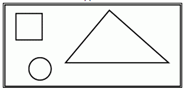
4. Перед нами толстая дощечка с тремя отверстиями: квадратным, треугольным и круглым (на рисунке дан вид сверху). Может ли существовать одна затычка такой формы, чтобы закрывать все эти отверстия? Если да, то опишите ее. Если нет — обоснуйте невозможность создания такой затычки.
5. Со стартовой площадки вылетел на север вертолет. Пролетев в северном направлении 100 км, он повернул на восток. Пролетев в эту сторону 100 км, вертолет сделал новый поворот — на юг и прошел в южном направлении 100 км. Затем он повернул на запад и, пролетев 100 км, опустился. Спрашивается: где расположено место спуска вертолета относительно стартовой площадки — к западу, к востоку, к северу или югу? Подсказка: Земля имеет форму, близкую к шару, а потому вертолет не вернется на стартовую площадку!
6. Сколько существует трехзначных натуральных чисел с четными цифрами, таких, что: а) цифры в числе не повторяются; б) цифры в числе могут повторяться; в) ровно две цифры в числе повторяются?
5 тур
1. Сможете ли вы найти четыре целых числа, сумма и произведение которых являются нечетными числами?
2. Первый вторник месяца Митя провел в Смоленске, а первый вторник после первого понедельника — в Вологде. В следующем месяце Митя первый вторник провел в Пскове, а первый вторник после первого понедельника — во Владимире. Сможете ли вы определить, какого числа и какого месяца Митя был в каждом из городов?
3. Сколько нечетных чисел заключено между 300 и 700?
4. Имеются 6 запертых чемоданов и 6 ключей к ним. При этом неизвестно, к какому чемодану подходит какой ключ. Сколько попыток вы попросите вам предоставить, чтобы наверняка открыть все чемоданы?
5. В турнире участвовали пять шахматистов. Известно, что каждый сыграл с остальными по одной партии и все набрали разное количество очков; занявший 1-е место не сделал ни одной ничьей; занявший 2-е место не проиграл ни одной партии; занявший 4-е место не выиграл ни одной партии. Определите результаты всех партий турнира.
6. Начнем считать пальцы на правой руке: первый — мизинец, второй — безымянный, третий — средний, четвертый — указательный, пятый — большой, шестой — снова указательный, седьмой — снова средний, восьмой — безымянный, девятый — мизинец, десятый — безымянный и т. д. Какой палец будет по счету 1992-м?
6 тур
1. Найдите, какую цифру обозначает каждая буква в следующем равенстве: АХА= БАХ.
2. Сколько нулей на конце этого числа: 1 ? 2 ? 3 ? 4... ? 50?
3. Некоторое число уменьшили на 7, потом уменьшили в 10 раз и получили число, которое на 34 меньше исходного. Найдите исходное число.
4. Яша идет от дома до школы 30 мин, а его брат Петя 40 мин. Петя вышел из дома на 5 мин раньше Яши. Через сколько минут Яша догонит Петю?
5. Пятиклассники ехали на автомашине из деревни в город. Когда они проехали 4/5 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути пятиклассники проделали пешком, затратив на это времени в 3 раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали пятиклассники на автомашине, чем шли пешком?
6. Сколько квадратов «спрятано» на рисунке?

7 тур
1. На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными? Ответ обоснуйте.
2. Разрежьте квадрат на пять треугольников так, чтобы площадь одного из этих треугольников равнялась сумме площадей оставшихся.
3. Дорога от дома до школы занимает у Пети 20 мин. Однажды по дороге в школу он вспомнил, что забыл дома ручку. Если теперь он продолжит свой путь с той же скоростью, то придет в школу за 3 мин до звонка, а если вернется домой за ручкой, то, идя с той же скоростью, опоздает к началу урока на 7 мин. Какую часть пути он прошел до того, как вспомнил о ручке?
4. 20 черных коров и 15 рыжих дают за неделю столько молока, сколько 12 черных коров и 20 рыжих. У каких коров больше удои: у черных или у рыжих? Ответ обоснуйте.
5. Если написать любое двузначное число, а затем поменять местами в этом числе цифры и вычесть из большего числа меньшее, то получится число, которое делится на 9. Почему?
6. Два лесоруба, Никита и Павел, работали вместе в лесу и сели завтракать. У Никиты было 6 лепешек, у Павла — 9. Тут к ним подошел охотник.
— Вот, братцы, заблудился в лесу, до деревни далеко, а есть очень хочется; поделитесь со мною хлебом-солью!
— Ну, что ж, садись; чем богаты, тем и рады, — сказали Никита и Павел.
15 лепешек были разделены поровну на троих. После завтрака охотник пошарил в карманах, нашел 15 р. и сказал:
— Не обессудьте, братцы, больше при себе ничего нет. Поделитесь, как знаете!
Охотник ушел, а лесорубы заспорили. Никита говорит:
— По-моему, деньги надо разделить поровну!
А Павел ему возражает:
— За 15 лепешек 15 р. И на лепешку приходится по рублю. У тебя было 6 лепешек, тебе 6 р., у меня 9 лепешек, мне 9 р.!
Кто из них сделал правильный расчет?
8 тур
1. Число увеличено на 25 %. На сколько процентов нужно уменьшить результат этого увеличения, чтобы получить первоначальное число?
2. Три бегуна — Антон, Сережа и Толя — участвуют в беге на 100 м. Когда Антон финишировал, Сережа находился в десяти метрах позади него, а когда финишировал Сережа — Толя находился позади него в десяти метрах. На каком расстоянии друг от друга находились Толя и Антон, когда Антон финишировал? (Предполагается, что все мальчики бегут с постоянными, но, конечно, не равными скоростями.)
3. Директор завода, рассматривая список телефонных номеров и фамилий своих сотрудников, заметил определенную взаимосвязь между фамилиями и номерами телефонов. Вот некоторые фамилии и номера телефонов из списка:

Какой номер телефона у сотрудника по фамилии Железнов?
4. На столе лежат в ряд пять монет: средняя — вверх орлом, а остальные — вверх решкой. Разрешается одновременно перевернуть три рядом лежащие монеты. Можно ли при помощи нескольких таких переворачиваний все пять монет положить вверх орлом? Ответ обоснуйте.
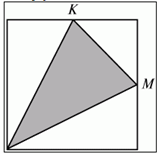
5. Точки К и М — середины сторон квадрата. Какую часть площадь закрашенного треугольника составляет от площади всего квадрата?
6. Сестре втрое больше лет, чем было брату тогда, когда сестре было столько лет, сколько брату теперь. Когда брату будет столько лет, сколько сестре сейчас, им обоим вместе будет 28 лет. Сколько сейчас лет сестре и сколько брату?
9 тур
1. По углам бассейна квадратной формы стоят четыре столба. Потребовалось расширить этот бассейн так, чтобы площадь его стала в два раза больше, а форма осталась бы квадратной. Можно ли это сделать, не убирая столбов, причем так, чтобы все столбы остались стоящими по периметру бассейна? Если можно, то как?
2. Докажите, что среди шести любых целых чисел найдутся два, разность которых делится на 5.
3. Внутренние покои дворца султана состоят из 100 одинаковых квадратных комнат, расположенных в виде квадрата 10x10. Если у двух комнат есть общая стена, то в ней обязательно есть ровно одна дверь. Сколько дверей во дворце?
4. Профессор Тестер проводит серию тестов, на основании которых он выставляет испытуемому средний балл. Закончив отвечать, Джон понял, что если бы он получил за последний тест 97 очков, то его средний балл составил бы 90; а если бы он получил за последний тест всего 73 очка, то его средний балл составил бы 87. Сколько тестов в серии профессора Тестера?
5. Ковбоя Джо приговорили к смертной казни на электрическом стуле. Ему известно, что из двух электрических стульев, стоящих в специальной камере, один неисправен. Кроме того, Джо известно, что если он сядет на этот неисправный стул, казнь не повторится и он будет помилован. Ему известно также, что стражник, охраняющий стулья, через день на все вопросы отвечает правду, а через день — ложь.
Приговоренному разрешается задать стражнику ровно один вопрос, после чего надо выбрать, на какой электрический стул садиться. Какой вопрос Джо может задать стражнику, чтобы наверняка выяснить, какой стул неисправен?
6. Найдите такие натуральные числа х, у, z, что
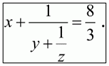
10 тур
1. Специально обученные собака и кошка участвуют в забеге: вперед по прямой до стены и обратно. Собака преодолевает за один прыжок 3 м, а кошка-только 2; но зато она делает 3 прыжка, в то время как собака делает 2. Скажите, каков при этих обстоятельствах возможный исход состязания, если до стены а) 12 м; б) 14 м; в) 15 м? Все ответы обоснуйте.
2. Один человек собирался построить дом и выяснил, что ему придется заплатить 1100 долларов обойщику и маляру, 1700 долларов маляру и жестянщику, 1100 долларов жестянщику и электрику, 3300 долларов электрику и плотнику, 5300 долларов плотнику и каменщику, 3200 долларов каменщику и маляру. Во сколько обошлось человеку строительство дома?
3. Найдите наименьшее натуральное число, которое, будучи разделено на 2, дает в остатке 1, при делении на 3 дает в остатке 2, при делении на 4 дает в остатке 3, при делении на 5 дает в остатке 4, при делении на 6 дает в остатке 5, но на 7 это число делится нацело.
4. Велосипедист, двигаясь по ветру, проезжает милю за 3 мин, а на обратном пути против ветра он преодолевает милю за 4 мин. Допустим, что он все время крутит педали с одинаковой силой, тогда, сколько ему понадобится времени, чтобы проехать милю при отсутствии ветра?
5. Один делец продал велосипед за 50 долларов, совершив тем самым эквивалентный обмен. Затем он выкупил его назад за 40 долларов, что, очевидно, принесло ему доход в 10 долларов, поскольку в итоге у него оказался тот же велосипед да еще 10 долларов впридачу. Далее, выкупив велосипед за 40 долларов, он продал его за 45 долларов, получив дополнительный доход в 5 долларов, так что общий доход составил 15 долларов.
— Постойте, — сказал бухгалтер. — Но ведь человек начал с велосипеда стоимостью в 50 долларов, а после вторичной продажи у него осталось 55 долларов. Как же он умудрился получить доход, превышающий 5 долларов? Ведь продав велосипед за 50 долларов, он просто совершил обмен, не получив дохода и не понеся убытков. Когда же он купил его за 40 долларов, а продал за 45 долларов, то получил при этом доход в 5 долларов. Вот и все.
— А я полагаю, — возразил счетовод, — что когда он продал велосипед за 50 долларов, а выкупил его за 40 долларов, то совершенно ясно, он получил доход в 10 долларов, ибо имел после этого тот же самый велосипед да еще 10 долларов. Но вот когда он вновь продал велосипед за 45 долларов, то просто совершил уже упомянутый ранее обмен, так что на этой операции у него не было ни дохода, ни убытков. Причем последняя операция не затронула первый доход; поэтому в итоге доход человека оказался равным 10 долларам.
Все эти операции крайне просты; относящиеся сюда подсчеты может сделать в уме любой первоклассник. И тем не менее перед нами три разных ответа! Который из них, по вашему мнению, правильный?
6. Решите уравнение
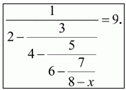
В ответе запишите значение выражения 161 ? х — 1.