Наименьшее общее кратное - урок 2 - ДЕЛИМОСТЬ ЧИСЕЛ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: формировать навык нахождения наименьшего общего кратного и наибольшего общего делителя; отрабатывать умение решать задачи алгебраическим способом; повторить теорию по теме «Делимость чисел».

Ход урока

I. Организационный момент

II. Сообщение темы урока

— Девизом сегодняшнего урока я взяла слова: «Нет ничего дороже для человека того, чтобы хорошо мыслить» (Л. Н. Толстой). Подтвердим это нашей работой на уроке.

— Продолжим находить наибольший общий делитель и наименьшее общее кратное нескольких чисел, повторим теорию по теме «Делимость чисел».

III. Устный счет

Цифровой диктант. (Можно проверить, выставив оценку.) Если утверждение, верно, пишите цифру 1, если нет - 0.

1. Делителем натурального числа а называют натуральное число, на которое а делится без остатка.

2. Цифры 0, 2, 4, 6, 8 — называют нечетными, а цифры 1, 3, 5, 7, 9 — четными.

3. Задачи, для решения которых рассматриваются все возможные комбинации, называют комбинаторными.

4. Если сумма цифр числа делится на 5, то и число делится на 5.

5. Если запись натурального числа оканчивается цифрой 3, то эго число делится без остатка на 3.

6. Число 1 является делителем любого натурального числа.

7. Числа, делящиеся без остатка на 2, называются четными.

8. Любое натуральное число имеет определенное количество кратных.

9. Комбинаторика - это раздел математики, занимающийся комбинаторными задачами.

10. Кратным натурального числа а называют натуральное число, которое делится с остатком на а.

11. Числа, которые при делении на 2 дают остаток 1, называются нечетными.

12. Если сумма цифр числа делится на 9, то и число делится на 9.

13. Число 1 — ни составное, ни простое число.

14. Натуральное число называют составным, если оно имеет только два делителя.

15. Натуральное число называют простым, если оно имеет только один делитель.

(Ответы. 1; 0; 1; 0; 0: 1; 0; 0; 1; 0; 1; 1; 1; 0; 0.)

IV. Работа над задачей

1. № 185 стр. 31 (самостоятельно).

Решение:

15 = 3 · 5; 20 = 2 · 2 · 5; 12 = 2 · 2 · 3;

НОК (15; 20; 12) = 20 · 3 = 60, следовательно, через 60 суток.

(Ответ: через 60 суток.)

2. № 199 стр. 32 (на доске и в тетрадях).

— Как найти среднее арифметическое?

— Можно сразу найти неизвестные числа? (Нет.)

— Каким способом будем решать задачу? (Алгебраическим.)

Решение:

1) Пусть х - второе число,

2x — первое число.

Зная, что среднее арифметическое двух чисел равно 54, составим уравнение:

(х + 2х) : 2 = 54

3х = 54 · 2

3х = 108

х = 108 : 3

х = 36; 36 - второе число.

2) 36 · 2 — 72 — первое число.

(Ответ: 72, 36.)

3. № 194 стр. 31 (коллективное обсуждение решения, самостоятельная запись решения, самопроверка).

— Назовите четные цифры. (2, 4, 6, 8, 0.)

— Какая цифра может стоять на первом месте в записи числа? (2, 4, 6, 8.)

— Какие цифры будут стоять на втором и третьем месте в записи числа? (Любая из пяти.)

— По правилу умножения получаем: 4 · 5 · 5 = 100 (чисел).

V. Физкультминутка

VI. Историческая справка

Слово «крат» — старинное русское слово (XI век), означающее «раз». Слово «многократно» означает «много раз».

Понятием кратного пользуются в жизненной практике при установлении вида года. Через каждые три обыкновенных года, в каждом из которых по 365 дней (в феврале 28 дней), бывает четвертый год, так называемый високосный, в котором 366 дней (в феврале 29 дней).

Если число, которым выражается указанный год, есть число, кратное 4, то указанный год високосный, а если не кратно 4, то год обыкновенный. Так. 2008 год — високосный, так как 2008 кратно 4, 2007 - не високосный, так как 2007 не кратно 4.

VII. Закрепление изученного материала

1. Устно. Фронтальная работа.

Найдите НОД и НОК чисел:

а) 5 и 15; б) 16 и 24: в) 16 и 10: г) 21 и 30;

д) 12 и 9; е) 3 и 5; ж) 36 и 9: з) 12 и 15.

2. № 180 (в, г) стр. 30 (самостоятельно в тетрадях, с последующей проверкой).

— Расскажите, как удобнее считать.

в) НОК (а; b) = 2 · 2 · 5 · 5 · 11 · 3 = 3300;

г) Так как b делится на а, то НОК будет само число b:

НОК (a; b) = 2 · 2 · 5 · 5 · 7 = 700.

3. № 181 (б, г, е) стр. 30 (один ученик на закрывающейся доске, остальные самостоятельно в тетрадях).

б) НОК (12; 16) = 2 · 2 · 2 · 2 · 3 = 48;

г) НОК (396; 180) = 2 · 2 · 3 · 3 · 11 · 5 = 1980;

е) НОК (168; 231; 60) = 231 · 22 · 2 · 5 = 9240.

— Кто не согласен с решением? Докажите, что ваш товарищ не прав.

VIII. Самостоятельная работа

Самопроверка. (На закрывающейся доске записаны ответы.)

Вариант I

1. Запишите по три общих кратных чисел:

а) 4 и 28; б) 5 и 6; в) 12 и 18.

2. Найдите наименьшее общее кратное чисел:

а) 18 и 27; б) 7875 и 4725.

Вариант II

1. Запишите по три общих кратных чисел:

а) 6 и 42; б) 7 и 4; в) 16 и 18.

2. Найдите наименьшее общее кратное чисел:

а) 40 и 56; б) 7425 и 4455.

IX. Повторение изученного материала

№ 196 стр. 32 (самостоятельно, ответы записывает один ученик на закрывающейся доске, самопроверка).

(Ответ: )

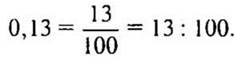X. Подведение итогов урока

— Чему равно наименьшее общее кратное взаимно простых чисел?

— Чему равно наименьшее общее кратное чисел, из которых одно делится на все остальные числа?

— Поступали ли мы в течение урока в соответствии с нашим девизом?

Домашнее задание

№ 202 (в, г, найти НОД и НОК), № 205 стр. 32, № 206 (б) стр. 33, № 145 (б) стр. 24.

Дополнительный материал

Старинная задана из «Арифметики...» Л. Ф. Магницкого.

Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, во сколько дней жена его отдельно выпьет ту же кадь.

Решение (предлагаемое в указанном учебнике, изданном в 17003 г.):

Рассмотрим 140 дней.

За это время один человек выпьет 140 : 14 = 10 бочонков,

а вместе с женою 140 : 10 = 14 бочонков.

Значит, за 140 дней жена выпьет 14 - 10 = 4 бочонка.

Один бочонок она выпьет за 140 : 4 = 35 дней.

(Ответ. 35 дней.)

Решите эту задачу с помощью понятия НОК двух чисел.