Перпендикулярные прямые - КООРДИНАТЫ НА ПЛОСКОСТИ - РАЦИОНАЛЬНЫЕ ЧИСЛА

Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости.

Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и угольника, не требуя воспроизведения точных определений.

Основным результатом знакомства учащихся с координатной плоскостью должны явиться знание порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным ее координатам, определить координаты точки, отмеченной на координатной плоскости.

Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.

ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ (2 ч)

Урок 145. Перпендикулярные прямые

Цели: ввести понятие и обозначение перпендикулярных прямых, перпендикулярных отрезков и лучей; показать способы построения перпендикулярных прямых; отрабатывать умение строить перпендикулярные прямые; воспитывать аккуратность.

Информация для учителя

Для построения прямых лучше использовать нелинованную бумагу.

Ход урока

I. Организационный момент

II. Анализ контрольной работы

1. Познакомить учащихся с результатами контрольной работы.

2. Выполнить работу над ошибками, решив задания, в которых допущено наибольшее количество ошибок, задания, вызвавшие затруднения у учащихся.

III. Устный счет

1. Решите уравнения:

8 + 32у = 10 + 31у (у = 2);

6 - 7х = 7 - 8х (х = 1);

2у + 4 = -6 + 3у (у = 10);

5 - 8у = 7 - 9у (у = 2)

2. За тетрадь и дневник мама заплатила 100 рублей. Дневник дороже тетради в 4 раза. Сколько стоит дневник? (80 руб.)

3. Какую часть часа составляют 20 минут?

IV. Индивидуальная работа

1 карточка

1. Раскрыть скобки и найти значение выражения:

4,23 - (3,24 + 8,4) + (1,6 - 4,23) + 3,24.

2. Решить уравнение: 2(7х — 4) — 2(2х — 3) = —39.

3. Привести подобные слагаемые: 12а - 17b + 13b - 12а + 2а.

4. Упростить выражение: -3(2а + 5с) + 4(с - 3а) - 2(-5а - 6с).

2 карточка

1. Раскрыть скобки и найти значение выражения:

4,49 - (6,21 + 3,3) + (6,7 - 4,49) + 6,21.

2. Решить уравнение: —7(3х — 8) + 3(4х + 5) = 8.

3. Привести подобные слагаемые: 23m — 21n + 16n — 13m — 16n.

4. Упростить выражение: —2(3а + 6с) + 8(с — а) —3(—6а — 7с).

V. Сообщение темы урока

— Сегодня для работы на уроке нам понадобится транспортир и чертежный треугольник. А вот зачем, вы узнаете в течение урока.

VI. Изучение нового материала

1. Подготовительная работа.

— Мыс вами знаем, что бывают разные линии. Сегодня мы узнаем, какие еще бывают прямые.

— Какие виды углов вы знаете? (Прямой, острый, тупой, развернутый.)

— Дайте определение прямого угла. (Угол, градусная мера которого равна 90°, называется прямым углом.)

— Как называется прибор для измерения углов? (Транспортир.)

2. Работа над новой темой.

— Постройте две пересекающиеся прямые.

— Обозначьте их.

— Сколько углов получилось при пересечении этих прямых?

— Что у них общего? (Общая вершина — тонка пересечения прямых.)

— Что можете сказать о парах этих углов? (Они равны.)

(Показать на чертеже.)

— Если все четыре угла равны между собой, то каждый угол равен 90°.

— Не по клеткам в тетради постройте две прямые так, чтобы при их пересечении получилось четыре прямых угла.

— Какие инструменты использовали при построении прямых? (Чертежный треугольник с прямым углом, транспортир.)

Определение. Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

— Это название произошло от латинского слова «perpendicularis», что означает «отвесный».

— Обозначают: a ⊥ b.

— Читают: прямая а перпендикулярна прямой b.

— Если a ⊥ b, то b ⊥ а.

— Постройте две перпендикулярные прямые a и c.

— Опишите взаимное расположение прямых: a ⊥ с.

— Отметьте по две точки на каждой прямой.

— Какие геометрические фигуры получились? (Отрезки и луни.)

— Что можете о них сказать? (Они перпендикулярны друг другу.)

— Опишите взаимное расположение отрезков: АВ ⊥ CD.

— Дайте определение перпендикулярных отрезков (лучей). Определение. Отрезки (или лучи), лежащие на перпендикулярных прямых, называют перпендикулярными.

— Для построения перпендикулярных прямых используют чертежный треугольник или транспортир. (Показать на доске построение прямых.)

VII. Закрепление изученного материала

1. В тетрадях проведите:

1) две перпендикулярные прямые, обозначьте их, запишите в тетрадь, что прямые перпендикулярны;

2) две прямые, перпендикулярные одной и той же третьей прямой.

2. № 1353 стр. 237 (устно).

с ⊥ b, k ⊥ l.

3. № 1354 стр. 237 (на доске и в тетрадях).

Вывод: через точку, не лежащую на прямой, можно провести только одну прямую, перпендикулярную данной прямой.

VIII. Физкультминутка

IX. Работа над задачей

№ 1361 стр. 238 (самостоятельно, устная проверка).

Решение:

1) 40% = 0,4

2) 200 · 0,4 = 80 (гр.) — нашел Никита.

3) 80 · 1/4 = 20 (гр.) — нашел Олег.

4) 200 - (80 + 20) = 100 (гр.) — нашел Дима.

(Ответ: 100 грибов.)

X. Повторение изученного материала

1. № 1358 (а, б) стр. 238 (самостоятельно, взаимопроверка).

— Сформулируйте правило переноса слагаемых из одной части уравнения в другую.

— Какое свойство уравнений использовали при решении второго уравнения?

а) 2х – 5 = х + 2

2х - х = 2 + 5

х = 7

1 способ

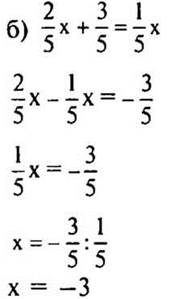
2 способ

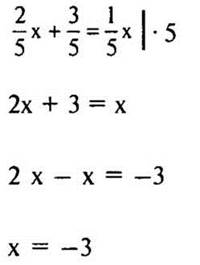
(Ответ: а) х = 7; б) х = —3.)

XI. Самостоятельная работа (10-15 мин)

Вариант I

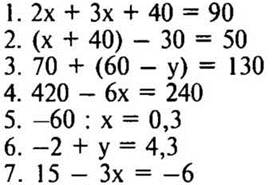
Вариант II

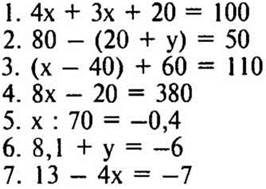
Критерии оценок:

«5» — верно решено 9—10 уравнений;

«4» — верно решено 7—8 уравнений;

«3» — верно решено 5—6 уравнений;

«2» — решено менее 5 уравнений.

XII. Подведение итогов урока

— Какие прямые называют перпендикулярными?

— Какие отрезки и лучи называют перпендикулярными?

— Сколько перпендикулярных прямых можно провести к данной прямой из одной точки, не лежащей на этой прямой?

Домашнее задание

№ 1365, 1366 стр. 239, № 1369 (в, г) стр. 240.