Поурочные разработки по Математике 6 класс
Сравнение чисел - ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА - РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели: рассмотреть правила сравнения положительных и отрицательных чисел; учить сравнивать рациональные числа.
Ход урока
I. Организационный момент
II. Устный счет
1. Решите уравнение:
1) | х | = 2; 2) | х | = 25; 3) | х | = —13.
2. В каком случае мы смотрим на 3, а говорим 15? (Часы.)
3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последний кусок? (9 марта.)
III. Индивидуальная работа
1 карточка
1. Запишите:
а) положительные числа, модули которых равны: 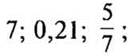
б) отрицательные числа, модули которых равны: 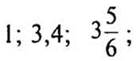
2. Найдите значение выражения:
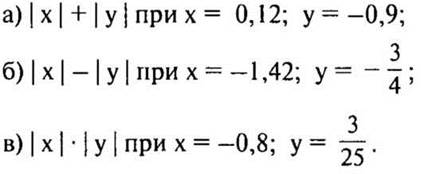
2 карточка
1. Запишите:
а) положительные числа, модули которых равны: 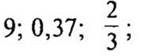
б) отрицательные числа, модули которых равны: 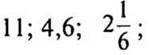
2. Найдите значение выражения:

3 карточка (для более подготовленных учащихся)
1. Запишите:
а) положительные числа, модули которых равны: 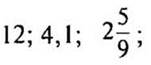
б) отрицательные числа, модули которых равны: 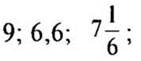
в) положительные и отрицательные числа, модули которых равны: 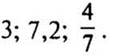
2. Найдите значение выражения:
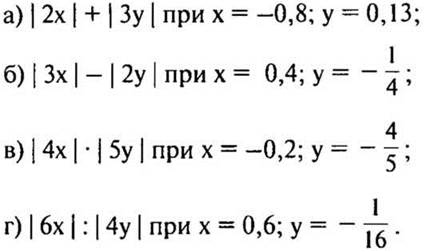
IV. Сообщение темы урока
— Сегодня на уроке мы будем учиться сравнивать положительные и отрицательные числа.
V. Изучение нового материала
1. Подготовительная работа.
а) Мы с вами умеем сравнивать положительные числа с помощью координатного луча.
— Вспомните это правило. (Большее число на координатном луче изображается точкой, расположенной правее, а меньшее число - левее.) (Луч направлен слева направо.)
Это правило распространяется на положительные и отрицательные числа. (Координатная прямая расположена горизонтально.)
б) Отметьте на координатной прямой точки с координатами -13; -1; 0; 9.
— Сравните:
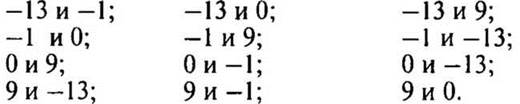
(Из двух чисел больше то, которое на координатной прямой расположено правее, меньше то, которое на координатной прямой расположено левее.)
— На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
2. Работа над новой темой.
— Запишите одно положительное и одно отрицательное число. Сравните. Сделайте вывод.
— Сравните отрицательное число и нуль. Сделайте вывод.
— Сравните положительное число и нуль. Сделайте вывод.
— Сравните два отрицательных числа. Сравните их модули. Сделайте вывод.
Правила сравнения чисел:
1. Любое отрицательное число меньше любого положительного.
2. Нуль больше любого отрицательного числа.
3. Нуль меньше любого положительного числа.
4. Из двух отрицательных чисел меньше то, модуль которого больше.
VI. Закрепление изученного материала
1. № 974 стр. 163 (на обратной стороне доски и в тетрадях).
— Как сравнивают числа с помощью координатной прямой?
— Ответ запишите в виде неравенства.
— Сравните свое решение с записями на доске.
2. № 979 стр. 165 (на доске и в тетради).
— Какие числа называются целыми?
— Ответ запишите в виде двойного неравенства.
Ответ:
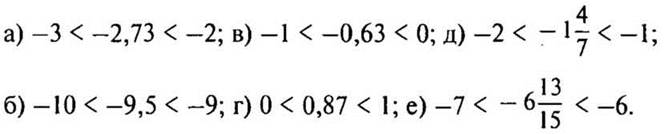
4. Сравните с нулем (устно):
— Как сравнить числа с нулем?
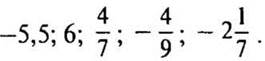
VII. Физкультминутка
VIII. Работа над задачей
№ 986 стр. 165 (на доске и в тетради).
Решение:
1) 730 — 380 + 460 = 810 (руб.) — у первого купца.
2) 970 — 460 + 380 = 890 (руб.) — у второго купца.
IX. Повторение изученного материала
1. № 982 стр. 165 (устно).
(Ответ: расстояние от дятла до белки равно 7, белка дальше от дупла.)
2. № 985 стр. 165 (устно).
— Какие точки будут иметь положительные координаты? (A, В.)
— Какие точки будут иметь отрицательные координаты? (С, D.)
(Ответы: В (2m); С (—m); D (—2m).)
X. Самостоятельная работа (3—4 мин)
Записать только ответы. Учащиеся под кальку записывают ответы. Один лист сдают учителю, другой оставляют себе. Затем сверяют свои ответы с правильными ответами на доске и сами оценивают свою работу.
Вариант I
1. Какие из чисел: —3 и —12 на координатной прямой расположены правее числа -7?
2. Найдите значение выражения:
![]()
3. Сравните модули чисел: а)-23 и 15; б) 41 и-13.
4. Сколько целых чисел расположено на координатной прямой между числами?
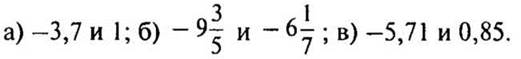
5. Найти значение выражения ![]()
Вариант II
1. Какие из чисел: —6 и —10 на координатной прямой расположены левее числа —8?
2. Найдите значение выражения:
![]()
3. Сравните модули чисел:
а) 17 и —15; б) -36 и 16.
4. Сколько целых чисел расположено на координатной прямой между числами?
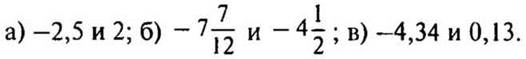
5. Найти значение выражения: ![]()
XI. Подведение итогов урока
— Как сравнивать числа с помощью координатной прямой?
— Как расположены на координатной прямой точки А(а) и В(b), если а меньше b? Если 0 больше b?
Домашнее задание
№ 995 стр. 167; № 992 (1), 994 (1) стр. 166.