Круговые диаграммы - урок 2 - IV ЧЕТВЕРТЬ

Оборудование: заранее написать решение задачи № 1677 на доске; два вида демонстрационных треугольников, транспортир; кодоскоп.

Ход урока

I. Проверка домашнего задания.

1. № 1677 - сверить решение задачи с записями на доске.

II. Практическая работа.

1. На доске изображены контуры двух видов треугольников.

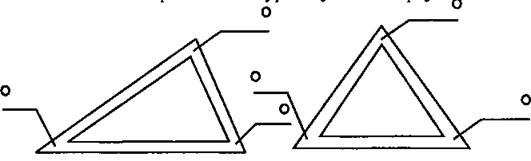
Ученик у доски измеряет углы на чертеже, другой измеряет углы непосредственно на треугольниках, за партами измеряют свои треугольники.

Ученики приходят к выводу, что существуют треугольники двух видов: с углами 90°; 60°; 30° и с углами 90°; 45°; 45°.

Вопросы учителя.

1. Чему равна сумма всех углов треугольника?

2. Как не имея транспортира, только при помощи треугольников, построить угол в 120°? 135°? 150°? 75°? 105°?

III. Устные упражнения.

1. № 1668 (в-д).

2. Проецируется на экран чертеж.

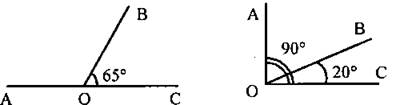
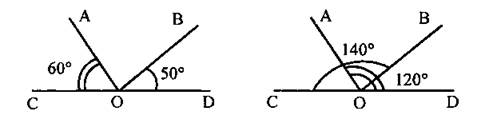
Вычислите градусную меру угла АОВ.

3. Вычислите неизвестные углы треугольника.

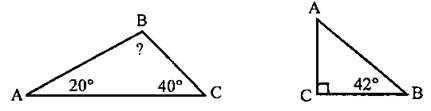
4. Найдите число, если 25% этого числа составляют 2; 10; 25; 0,5; 1,2.

5. Сколько процентов составляет:

а) 8 кг от 1 ц; б) 15 с от 1 мин; в) 35 см от 1 м?

IV. Работа по теме урока.

1. № 1667, 1664.

2. На повторение № 1676.

3. Самостоятельная работа (обучающая, посадить парами «сильный - слабый»).

а) Постройте углы РОК и SED, если РОК - 27°, a SED = 127°.

б) Луч CD разделил угол FCK на два угла FCD и DCK. Угол DCK равен 99° и составляет 9/11 угла FCK. Найдите градусную меру углов FCK и FCD.

в) Из одной точки В проведены лучи ВС, ВА и BD так, что ABC = 150° и ABD = 90°. Какую градусную меру может иметь CBD?

V. Домашнее задание: п. 43; № 1678, 1679, 1681. Прочитать об истории развития геометрии. Подготовиться к контрольной работе.