Математика 5 класс - Поурочные разработки
Площадь фигур, составленных из прямоугольников - Площадь прямоугольника - Треугольники и четырехугольники
Цель: научить находить площади фигур, составленных из прямоугольников.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите: 32, 72, 82, 1002, 52, 102, 12, 42, 10002.
2. Вычислите недостающие данные и найдите периметр фигуры (рис. 137).
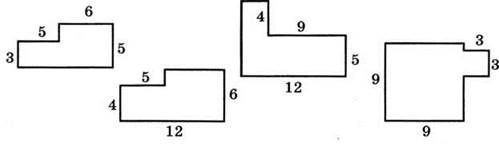
Рис. 137
III. Формирование умений и навыков.
1. РТ, часть 2, № 99, 100, 101.
2. У, № 685, 686, 687.
3. У, № 690. Задача решается практически. Надо предложить учащимся начертить в тетради произвольный прямоугольник (квадрат). Уменьшить (увеличить) сторону прямоугольника (квадрата) в 3 раза (вдвое) и начертить новый прямоугольник (квадрат). Легко видеть, что площадь исходного прямоугольника (квадрата) в 3 (4) раза больше (меньше) площади получившегося.
4. У, № 693. Площадь цветного квадрата равна половине площади всего квадрата. Надо вырезать квадрат из листа бумаги и загнуть белые треугольники к центру, наложив их на цветные. Мы получим два равных квадрата — белый и цветной.
5. У, № 692. Сумма длин смежных сторон данного прямоугольника равна 8 см. Это могут быть прямоугольники со сторонами 1 см и 7 см, 2 см и 6 см, 3 см и 5 см, 4 см и 4 см. Площади этих прямоугольников соответственно равны 7 см2, 12 см2, 15 см2 и 16 см2. Значит, длины сторон искомого прямоугольника равны 3 см и 5 см.
Физкультминутка «Истинно — ложно»
Если высказывание верное, то поверните голову налево, если ложное — направо. ® Площадь квадрата со стороной 4 см равна 16 см.
• Площадь квадрата со стороной 2 см равна 8 см.
• Развернутый угол в 3 раза больше прямого.
• Периметр квадрата со стороной 2 см равен 8 см.
• Диагональ разбивает прямоугольник на 2 равных треугольника.
• В тупоугольном треугольнике все углы тупые.
• Любой квадрат является прямоугольником.
6. Проверочная работа. КР, с. 32, варианты 1, 2. Дополнительно: У, № 691 (а, б) — по вариантам.
IV. Итоги урока.
1. Как найти площадь всей фигуры, зная площади всех ее частей?
2. Как найти площадь фигуры, состоящей из прямоугольников?
V. Домашнее задание.
У, № 684, 689.