ЧИСЛА ОТ 0 ДО 100 - Вторая четверть - ЧАСТЬ 1 УЧЕБНИКА

В данном разделе учащиеся знакомятся с устной и письменной нумерацией чисел от 21 до 100 и приемами сложения и вычитания этих чисел, включая письменные способы вычислений.

Согласно принятой программе изучение нумерации чисел в пределах сотни проводится в два этапа: сначала изучается нумерация чисел от 11 до 20, а затем нумерация чисел от 21 до 100. Это обусловлено особенностями в образовании числительных, обозначающих в русском языке числа от 21 до 100.

Для названий чисел от 11 до 20 употребляются сложные имена числительные, первая часть слова которых обозначает число отдельных единиц, а вторая «дцать» — десяток. Образование числа происходит на основе сложения: 10 + 3 = три-на-дцать — три единицы да еще десяток.

Для названий круглых десятков употребляют сложные имена числительные, обозначающие количество десятков в числе. Образование числа происходит на основе умножения: 30 = 3 · 10 = три-дцать = 3 раза по десять или три десятка. Исключение: сорок, девяносто.

А вот названия остальных двузначных чисел образуются на основе употребления составных имен числительных, состоящих из двух слов: первое слово обозначает разряд десятков, а второе — разряд единиц. Образование этих чисел происходит на основе умножения и сложения: 34 = 3 · 10 + 4 = три-дцать-четыре = 3 десятка да еще 4 единицы.

Главное при изучении устной нумерации чисел от 11 до 100 — раскрыть их десятичный состав. Отсчитывая 10 палочек и завязывая их в пучок, получаем 1 десяток. Далее ведется счет десятками: 1 десяток, 2 десятка, 3 десятка, ... , 9 десятков. Учащиеся знакомятся с понятием разряда и принципами образования, называния и записи двузначных чисел.

Письменная нумерация двузначных чисел строится на основе поместного значения цифр. Поэтому важно довести до сознания детей, что одна и та же цифра может иметь разное значение в записи числа в зависимости от места, которое она в этой записи занимает. Например, цифра 3 может обозначать 3 единицы, если находится на первом месте справа, и 3 десятка, если находится на втором месте справа. Для обозначения отсутствия единиц в первом разряде при записи двузначного числа на месте разряда единиц пишется 0.

Весьма полезным для начала обучения нумерации чисел от 21 до 100 является использование наглядных пособий, среди которых особую роль играют счеты и абак — наглядное пособие в виде лент с прорезями для цифр или знаков, их заменяющих, таблицы с кармашками и т. п. (см. рис.).

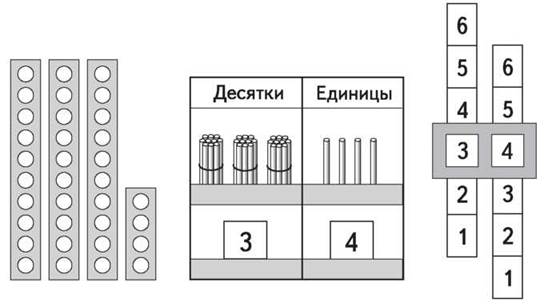
Демонстрируя число на каком-нибудь из этих пособий, учитель спрашивает: «Сколько десятков? (3.) Какое это число? (30.) Сколько единиц? (4.) Какое число изображено на полотне? (34.)»

Желательно, чтобы и у учащихся были индивидуальные абаки и счеты, на которых дети по заданию учителя составляют названное число, например 45, 23, 57 и др., и анализируют его десятичный состав.

Образование двузначных чисел путем прибавления и вычитания единицы удобно демонстрировать с помощью счетов.

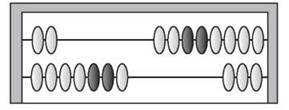
— Какое число отложено на счетах с помощью косточек? (27.) Прибавляйте по одному к этому числу и следующим числам, называйте эти числа. (28, 29, 30, 31, 32.)

— Отложите на счетах число 72. Вычитайте из него каждый раз по одному. Называйте полученные числа до 65. (71, 70, 69, 68 и т. д.)

Ознакомление с приемами устных вычислений ведется в основном с опорой на наглядность (счеты, абак, десятки — пучки палочек и единицы — отдельные палочки). Поэтому всякий раз, когда у учащихся возникают трудности в понимании вычислительного приема или ошибки в вычислениях, им надо дать возможность воспользоваться этими пособиями и не на абстрактном, а на наглядном и даже предметном уровне выполнить действия.

Такой подход к раскрытию смысла того или иного вычислительного приема снимает вопрос о необходимости формального введения некоторых свойств арифметических действий, на которых тем не менее эти приемы основаны.

Так, сочетательное свойство сложения в учебнике не рассматривается. Вместо него в 3 классе будут введены правила прибавления числа к сумме и суммы к числу.

На данном же этапе учащиеся должны уяснить суть приемов, исходя из действий со счетным материалом и предметными множествами с опорой на наглядность и здравый смысл. Так, оперируя с пучками палочек, учащиеся сами приходят к выводу о наиболее удобном способе вычислений, когда, например, получается круглое число или одно из слагаемых удобно заменить суммой двух чисел. При этом знание таблицы умножения и умение вести счет десятками до 100 обеспечивает введение приемов умножения и деления круглых чисел.

Желательно, чтобы учащиеся при первоначальном ознакомлении с приемом вычислений давали подробные объяснения выполняемым действиям. По мере того как прием будет усвоен, эти рассуждения можно постепенно сокращать. Например: «Десятки складывают с десятками, а единицы — с единицами; единицы вычитают из единиц, а десятки — из десятков». Такие пояснения будут даваться, например, при вычислении сумм вида 35 + 2, 60 + 34 или разностей вида 56 - 20, 56 - 2.

В учебнике каждый новый вычислительный прием иллюстрируется с помощью пучков палочек и отдельных палочек, а также сопровождается подробными пояснениями и записями, в том числе и с использованием письменных вычислений. Это позволяет учащимся не только лучше понять и усвоить алгоритм вычислений на оперативном уровне, но и научиться проводить рассуждения. Вообще говоря, на уроках математики необходимо постоянно уделять внимание развитию осознанной и грамотной математической речи учащихся, тем более что при изучении данных вычислительных приемов в концентре «Сотня» создаются наиболее благоприятные возможности: рассуждения становятся более развернутыми и аргументированными. Но для того чтобы сформировать у учащихся умение комментировать и обосновывать выполняемые действия, необходима организация систематической работы по обучению доказательным рассуждениям сначала в более простых ситуациях, когда используются так называемые одношаговые рассуждения, и с опорой на специальные памятки в виде плана или схемы рассуждений.

Например, при изучении письменных приемов сложения в пределах 100 весьма эффективна памятка для рассуждений в виде плана с указанием управляющих слов: «1) Пишу пример в столбик. 2) Складываю единицы. 3) Складываю десятки. 4) Читаю ответ». Проводя такие рассуждения, учащиеся лучше усваивают структуру объяснения вычислений и непосредственно сами приемы сложения и вычитания чисел в пределах 100.

Важное место на этих уроках занимает отработка умений выполнять проверку действий сложения и вычитания, которая включает как устные, так и письменные приемы вычислений.

Знакомство с единицами времени (час, минута) способствует уточнению временных представлений детей. Необходимо сформировать у учащихся конкретные представления о каждой единице времени, добиваться усвоения соотношений, научить пользоваться часами и с их помощью решать несложные задачи на вычисление продолжительности события, если известны его начало и конец. Большое воспитательное значение имеют примеры из жизни, данные о том, сколько продукции выпускают заводы (фабрики) за 1 минуту, за 1 час, за 1 рабочий день. В результате изучения этой темы учащиеся должны научиться определять время по часам и вести отсчет времени с точностью до часа, минуты.

Во втором полугодии продолжается знакомство учащихся с числовыми выражениями и правилами порядка действий. Вводятся выражения со скобками, рассматриваются текстовые задачи, математическими моделями которых являются выражения со скобками. Учащиеся знакомятся с новой формой записи решения задачи в виде числового выражения.

Обобщаются представления учащихся о геометрических фигурах и величинах. Знакомству с новой единицей длины — метром предшествуют уроки, на которых учащиеся рассматривают старинные меры длины, учатся пользоваться ими для измерения длин конкретных предметов и выясняют, что эти меры не являются универсальными, ибо не обеспечивают однозначности результатов измерений. Весьма полезно на этих уроках познакомить детей с этимологией некоторых старинных русских мер длины. Например, слово сажень произошло от старославянского сажичти (протягивать руку), а слово верста — от слова вертеть, ибо первоначально означало оборот плуга, т. е. расстояние, пропахиваемое за один раз в одну сторону; в свою очередь, вершком на Руси называли отверстие в избе, через которое выходил дым, возможно, поэтому как единица длины это слово означает верхнюю фалангу указательного пальца.

После ознакомления с понятием длины ломаной как суммы длин ее звеньев, введения понятия прямого угла и уточнения представлений о свойствах прямоугольника, квадрата учащиеся переходят к решению задач на вычисление периметра многоугольника. Таким образом, на данном этапе геометрическая линия в курсе 2 класса получает определенное и вполне логичное завершение.

В конце второго полугодия несколько уроков отводится на ознакомление с задачами на увеличение (уменьшение) числа в несколько раз. Эти задачи являются, с одной стороны, объектом изучения и формирования смысла отношений «больше в ...», «меньше в ...», а с другой стороны — связующим звеном между теорией и практикой обучения и средством развития познавательных способностей учащихся.

В процессе обучения решению этих задач у учащихся должны быть отработаны умения, связанные с конкретными этапами работы: умение читать задачу (понимать значения слов в ней, выделять главные (опорные) слова); умение выделять условие и вопрос задачи, известное и неизвестное (данные и искомое); умение устанавливать связь между данными и искомым, т. е. проводить разбор задачи (анализ ее текста), результатом которого является выбор арифметического действия для решения задачи; умение записывать решение и ответ задачи.

Решение задач на увеличение и уменьшение в несколько раз опирается на хорошее понимание конкретного смысла действий и деления умножения и смысла выражений «больше в ...», «меньше в ...».

Следовательно, подготовительная работа и должна быть направлена на изучение этих вопросов. Для раскрытия смысла выражений «больше в ...», «меньше в ... » целесообразно выполнить ряд упражнений, подобных следующим:

— Положите рядом 4 кружка, а справа 2 раза по 4 кружка. В таком случае говорят, что справа кружков в 2 раза больше, чем слева, потому что справа 2 раза по столько кружков, сколько их слева, а слева в 2 раза меньше, чем справа, — слева один раз по 4 кружка.

— Положите в ряд 2 квадрата, а справа 3 раза по 2 квадрата. Что можно сказать о числе квадратов справа: их больше или меньше, чем слева? (Их в 3 раза больше, чем слева, а слева в 3 раза меньше, чем справа.)

— Положите справа в ряд 3 треугольника, а слева в 4 раза больше. Что это значит? (По 3 треугольника взять 4 раза.) Что можно сказать о числе треугольников справа: их больше или меньше, чем слева? (Их в 4 раза меньше.)

После выполнения нескольких подобных упражнений можно приступить к решению задач.

— Положите в один ряд 5 квадратов, а в другой в 2 раза больше. Как вы это сделаете? (Положим 2 раза по 5 квадратов.) Сколько всего квадратов во втором ряду? (10.) Как узнали? (5 умножили на 2.)

Раскрытие смысла слов «больше в ...» , «меньше в ...» и первичное ознакомление с решением простых задач на увеличение (уменьшение) числа в несколько раз желательно провести с опорой на наглядность и действия с предметными множествами.

— Для детского сада купили зеленые и красные мячи. Зеленых мячей купили 4 штуки. (Учитель выставляет на наборном полотне 4 зеленых кружка.)

— А красных мячей купили в 3 раза больше, чем зеленых. Как это количество изобразить с помощью красных кружков? Что значит в 3 раза больше, чем зеленых? (Их 3 раза по 4 мяча.)

— Изобразим эти мячи. (Учитель выставляет на наборном полотне под зелеными кружками 3 раза по 4 красных кружка. При этом он говорит: «Первый раз по 4, второй раз по 4 и третий раз по 4.)

— Можем мы теперь узнать, сколько красных мячей купили? (Да.) Как мы это узнаем? (4 · 3.) Сколько получится? (12 мячей.)

— Запишем решение задачи. Повторите, как узнать, сколько красных мячей купили. (4 · 3 = 12.) Назовите ответ. (12 мячей.)

Заметим, что в учебнике предлагается и другая форма иллюстрации задач на увеличение (уменьшение) числа в несколько раз, когда активно используется числовой луч. Такой же подход был реализован и в 1 классе при рассмотрении отношений «больше на ...», «меньше на ...».

В результате многократного решения таких задач учащиеся должны усвоить, что увеличение числа в несколько раз выполняется действием умножения, а уменьшение числа в несколько раз — действием деления.

Заметим, что решение задач на увеличение (уменьшение) числа в несколько раз надо по возможности чаще рассматривать в сопоставлении с решением задач на увеличение (уменьшение) числа на несколько единиц, чтобы предупредить формирование у учащихся возможных ошибочных ассоциаций.