Путешествие в историю математики - Свечников А. А. 1995

Несколько старинных приемов вычислений

Проверка девяткой

В Древней Индии математические вычисления обычно выполняли тонкой палочкой на доске, покры­той песком, при этом довольно ча­сто приходилось записанную ра­нее цифру стирать и записывать на ее место новую, полученную при вычислениях. Но проверить по сохранившейся на доске запи­си результат вычисления было

довольно сложно. Индийские вы­числители нашли иной способ проверки действий — проверку девяткой. Впоследствии прожи­вавшие в Средней Азии арабы позаимствовали у индийцев их нуме­рацию и многие приемы вычисле­ний, в том числе и проверку де­вяткой.

Проверка девяткой основана на том, что остаток от деления чи­сла на 9 равен остатку от деления на 9 суммы значений цифр данно­го числа. Например, 372 : 9 = 41 (остаток 3); сумма значений цифр этого числа 3 + 7 + 2 = 12; при делении 12 на 9 образуется тоже остаток 3.

Математики Востока ввели да­же особое «мерило»» — укорочен­ное число, которое облегчало проверку действия. Укороченное число (мерило, или остаток при делении числа на 9) находили сложением значений всех цифр данного числа. Так, для числа 372 сумма значений цифр состав­ляет 12, а для 12 — 3(1 + 2 = 3), следовательно, мерило (или укороченное число, или остаток) при делении на 9 для числа 372 будет 3. Для числа 8695 : 8 + 6 + 9 + 5 = 28; 2 + 8 = 10;

1 + 0 = 1, т. е. укороченное число равно 1.

Приведем примеры проверки девяткой различных действий.

1. Сложение.

577 + 439 = 1016.

Сумма значений цифр слагае­мых

(5 + 7 + 7) + (4 + 3 + 9) = 35.

Укороченное число для 35 бу­дет: 3 + 5 = 8.

Следовательно, при делении суммы значений цифр слагаемых на 9 получаем в остатке 8, и уко­роченное число суммы (1016) то­же 8. Ошибки при сложении не обнаружено.

2. Умножение.

365 • 56 =20 440.

Для проверки девяткой нахо­дим укороченные числа множите­лей, т. е. для 365 : 3 + 6 + 5 = 14 и 1 + 4 = 5; для 56 : 5 + 6 = 11, 1 + 1 = 2; умножаем укорочен­ные числа множителей 5 • 2=10, находим укороченное число произведения: 1 + 0=1. Срав­ниваем его с укороченным чис­лом для 20 440, т. е. 2 + 0 + 4 + 4 + 0 = 10, 1 + 0 = 1. Остатки при делении на 9 произ­ведения и множителей совпада­ют. Ошибки не обнаружено.

3. Вычитание.

794 - 359 = 435.

Найдем укороченные чис­ла. Для 794 : 7 + 9 + 4 = 20, 2 + 0 = 2; для 435 : 4 + 3 + 5 = 12, 1 + 2 = 3; для 359 : 3 + 5 + 9 = 17, 1 + 7 = 8. Найдем укороченное число при сложении остатка с вычитаемым, т. е. 8 + 3 = 11,1 + 1 = 2. При де­лении на девятку остаток в пер­вом случае (для 794) 2 и в послед­нем (для 435 и 359) тоже 2. Ошиб­ки в действии вычитания не обна­ружено.

4. Деление. Порознь для част­ного и делителя находим укоро­ченные числа. Умножим их и най­дем для их произведения укоро­ченное число. Сравним его с укороченным числом делимого из за­данного примера. Если они не рав­ны, то при делении допущена ошибка.

775 : 25 = 31.

Проверка: укороченное чи­сло частного: 3 + 1 =4. Укоро­ченное число делителя: 2 + 5 = 7. Произведение найденных укоро­ченных чисел 4 • 7= 28. Укоро­ченное число для 28 : 2 + 8 = 10 или 1 + 0 = 1. Укороченное число делимого: 7 + 7 + 5= 19 или 1 + 9 = 10, 1 + 0 = 1.

Проверка показала: найденные укороченные числа равны, сле­довательно, ошибка не обнару­жена.

Проверка девяткой широко применялась в XV в. и позже. Спо­собы проверки девяткой реко­мендовал применять и Л. Ф. Маг­ницкий в «Арифметике». Однако он не указал, что эта проверка не всегда позволяет уловить ошиб­ку, допущенную при вычислениях, например при ошибочной пере­становке цифр.

Два способа умножения чисел

Умножение долгое время счита­лось трудной операцией. Многие математики в XVI в. пытались отыскать более легкий прием ум­ножения, и появилось несколько вариантов умножения. Тогда же был открыт и современный метод под названием «шахматный спо­соб умножения».

В старину многие при умноже­нии пользовались способом умно­жения решеткой. Для этого один из множителей записывали гори­зонтально с увеличенными промежутками между цифрами. Под ним вычерчивали решетку в виде клеток, причем каждую клетку делили наклонной линией на два треугольника. Второй множитель располагали справа от решетки и записывали число вертикально сверху вниз, располагая цифры строго против клеток решетки.

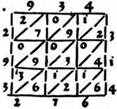
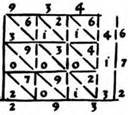
Умножим способом решетки 572 на 361. Умножать начнем с наивысших разрядов. Когда от ум­ножения пары цифр получим од­нозначное число, запишем его в нижней части клетки, а в верхней части напишем нуль. Если же по­лучим двузначное число, то де­сятки его запишем в верхней ча­сти клетки, а единицы — в ниж­ней. Когда все пары множителей будут умножены и результаты за­писаны в решетке, произведем сложение цифр отдельно для ка­ждой наклонной полосы. Сложе­ние выполним справа налево. Если при сложении получится сумма двузначная, то запишем только единицы, а десятки приба­вим к сумме чисел слева от на­клонной полосы. Произведение окажется записанным слева от решетки и внизу нее. Прочитаем ответ: 206 492.

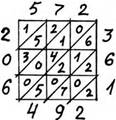
В Италии этот способ умноже­ния называли джелозия, что оз­начает «оконные жалюзи» — ре­шетка.

А вот еще один способ умноже­ния, не утративший своего значе­ния и в наши дни. В «Арифметике» Л. Ф. Магницкого, в главе, посвя­щенной умножению, читаем: «Нецыи же умножают странным иным некоим образом... якоже зде умножено есть зри сице

В приведенном способе умно­жение начато с высших разрядов, а не с низших. В этом и состоит «странность» этого способа.

Академик А. Н. Крылов (1863 — 1945) — один из крупнейших мате­матиков и вычислителей — на­стойчиво советовал начинать ум­ножение с высших разрядов. Осо­бенно следует рекомендовать этот способ при выполнении приб­лиженных вычислений, так как он экономичнее и удобнее обычно­го — в этом случае при первом же умножении мы получаем важней­шую часть произведения.