Применение векторов к решению задач - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ

Цели: на конкретных примерах показать применение векторов при решении геометрических задач; развивать логическое мышление учащихся, учить решать задачи.

Ход урока

I. Анализ результатов самостоятельной работы.

1. Указать ошибки учащихся при выполнении работ.

2. Решить задачи, вызвавшие затруднения у учащихся.

II. Повторение изученного материала.

1. Ответить на вопросы на с. 213–214.

2. Вспомнить основные правила действий с векторами.

3. Решить задачи на доске и в тетрадях:

1) Упростите выражение

2) Найдите вектор из условия

4. Записать в тетрадях таблицу перевода с «геометрического» языка на «векторный»:

C – точка на прямой AB
MN || PQ
M – точка на отрезке AB, такая, что AM : MB = л
ABCD – параллелограмм
ABCD – трапеция (AB || CD)

III. Работа по учебнику.

1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.

2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.

IV. Решение задач.

1. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что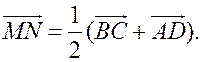

Решение

Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем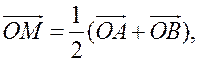 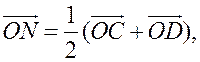поэтому .

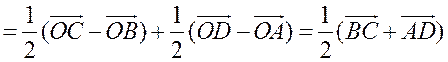Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.

2. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство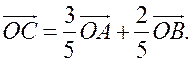

Решение

По условию AC : CB = 2 : 3, поэтому Но Следовательно, откуда получается

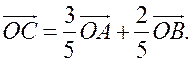
Примечание. Задача 3 является частным случаем более общей задачи 806.

3. Решить задачу № 784 на доске и в тетрадях.

4. Решить задачу № 786 на доске и в тетрадях.

Решение

Так как точка А1 – середина стороны ВС, то .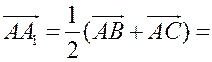

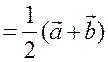Далее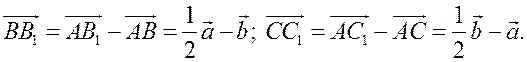

5. При наличии времени решить задачу 4.

Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.

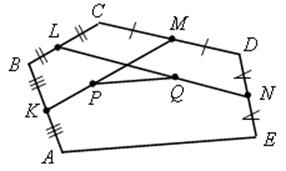
Решение

Пусть О – произвольная точка. Согласно задаче 1 из п. 84 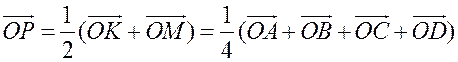. Аналогично, .

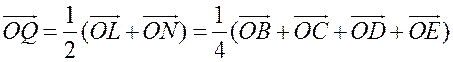Из этих равенств следует, что 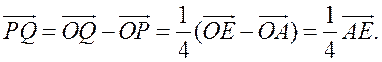Отсюда следует, что PQ || AE и PQ = AE.

V. Итоги урока.

Домашнее задание: повторить материал пунктов 76–84; разобрать решения задачи 2 из п. 84 и задачи № 788 и записать в тетрадь; решить задачу № 785.