Поурочные разработки по геометрии 9 класс
Длина окружности - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА
Цели: вывести формулу, выражающую длину окружности через ее радиус; вывести формулу для вычисления длины l дуги окружности с градусной мерой ; закрепить знание формул при решении задач.
Ход урока
I. Математический диктант (15 мин).
Вариант I
1. Найдите угол правильного десятиугольника.
2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2 м.
3. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м.
4. Найдите площадь правильного треугольника, если расстояние от его центра до вершины равно 2 м.
5. Закончите предложение: «Угол с вершиной в центре окружности называется …»
6. Угол с вершиной в центре правильного многоугольника и сторонами, проходящими через две его соседние вершины, равен 36°. Сколько сторон имеет этот многоугольник?
7. Чему равен cos 0°?
8. С помощью циркуля и линейки постройте правильный шестиугольник.
Вариант II
1. Сколько сторон имеет правильный многоугольник, если его сторона стягивает дугу описанной окружности, равную 18°?
2. Найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм.
3. Закончите предложение: «Кругом называется часть плоскости …»
4. Найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм.
5. Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2 дм.
6. Чему равен cos 0°?
7. Найдите угол правильного девятиугольника.
8. С помощью циркуля и линейки постройте правильный треугольник.
II. Изучение нового материала (лекция).
Поскольку материал пункта «Длина окружности» нетрадиционен и опирается на понятие предела, его изложение целесообразно дать в форме лекции.
1. Дать представление о длине окружности с помощью нитки, обмотанной около дна стакана.
2. Работа по рисункам 312 и 313 учебника.
3. Вывод формулы, выражающей длину окружности через ее радиус.
4. Записать в тетради вывод: отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Число π (пи).
5. Формула для вычисления длины окружности: C = 2πR; d = 2R, тогда C = πd, где d – диаметр окружности.
Найдем радиус и диаметр окружности: R = ![]() ; d =
; d = ![]() , где π ≈ 3,14.
, где π ≈ 3,14.
6. Вывод формулы для вычисления длины l дуги окружности с градусной мерой :
длина дуги в 1° равна 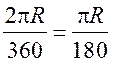 ; длина дуги в ° равна l =
; длина дуги в ° равна l = ![]() ∙ .
∙ .
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 1101 (таблицу начертить заранее на доске).
2. Устно решить задачи № 1102 и № 1103.
3. Решить задачу № 1109 (а, б).
4. Решить задачу № 1111 (использовать рис. 316).
IV. Итоги урока.
Домашнее задание: изучить материал пункта 110; решить задачи №№ 1109 (в, г), 1106, 1104 (а), 1105 (а).