Поурочные разработки по геометрии 9 класс
Решение треугольников - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
Цели: познакомить учащихся с методами решения треугольников; закрепить знание учащимися теорем синусов и косинусов, научить применять эти теоремы в ходе решения задач.
Ход урока
I. Проверка изученного материала.
Учащиеся на отдельных листочках доказывают изученные теоремы и сдают учителю.
Вариант I
Сформулируйте и докажите теорему косинусов.
Вариант II
Сформулируйте и докажите теорему о площади треугольника.
Вариант III
Сформулируйте и докажите теорему синусов.
II. Изучение нового материала.
1. Решением треугольника называется нахождение всех его шести элементов (то есть трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
2. При решении треугольников используют теоремы синусов и косинусов, причем при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов. Например, зная три стороны треугольника, для вычисления первого угла применяем теорему косинусов, а для вычисления второго угла можно использовать как ту, так и другую теоремы. Но поскольку синус угла равен синусу смежного с ним угла, то нахождение синуса угла еще не позволяет определить сам угол – он может быть острым или тупым. Если же вычислить косинус угла, то по его знаку и величине угол определяется однозначно.
3. Рассмотрим три задачи на решение треугольника:
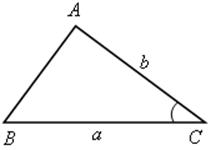
1) решение треугольника по двум сторонам и углу между ними;
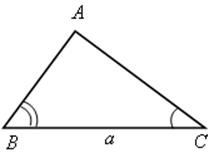
2) решение треугольника по стороне и прилежащим к ней углам;
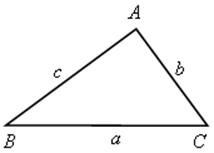
3) решение треугольника по трем сторонам.
При этом будем пользоваться следующими обозначениями для сторон треугольника АВС: АВ = с; ВС = а; СА = b.
4. В тетрадях учащиеся оформляют таблицу-памятку:
|
|
|
c = cos A =
|
b = c = |
cos A = cos B =
|
III. Решение задач.
1. По рисунку 294 учащиеся самостоятельно разбирают решение примера на странице 259 учебника.
2. Решить задачу № 1025 (б, в, г, ж, и) на доске и в тетрадях, используя таблицы Брадиса и микрокалькуляторы.
3. Решить задачу № 1021 на доске и в тетрадях.
4. Совместно с учащимися разобрать и зафиксировать в тетрадях решение задачи № 1033 по рисунку 297.
5. Решить задачи № 1060 (в), 1061 (в) и 1062.
IV. Итог урока.
Задание на дом: изучить материалы пунктов 96–99; решить задачи №№ 1025 (а, д, е, з), 1060 (г), 1028.
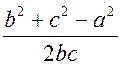 ;
;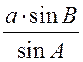 ;
;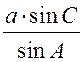
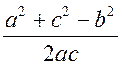 ;
;