Поурочные разработки по геометрии 9 класс
Синус, косинус, тангенс. Основное тригонометрическое тождество - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
Урок 1. Синус, косинус, тангенс. Основное тригонометрическое тождество
Цели: повторить определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; ввести понятия синуса, косинуса и тангенса для углов от 0° до 180° и закрепить их знание в ходе решения задач.
Ход урока
I. Повторение ранее изученного материала.
1. Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
2. Какое равенство называют основным тригонометрическим тождеством?
3. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45° и 60°?
II. Изучение нового материала.
1. Ввести понятие единичной полуокружности (рис. 290).
2. Ввести понятие синуса и косинуса для углов 0° ≤ ≤ 180°:
sin = y; соs = х.
Таким образом, для любого угла б из промежутка 0° ≤ ≤ 180° синусом угла б называется ордината у точки М, а косинусом угла б – абсцисса х точки М, лежащей на единичной полуокружности.
0 ≤ sin ≤ 1; cos ≤ 1.
3. Нахождение значений синуса и косинуса для углов 0°, 90° и 180°.
4. Определение тангенса угла ( ![]() 90°):
90°):
tg = 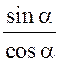 при
при ![]() 90°; tg 0° = 0; tg 180° = 0.
90°; tg 0° = 0; tg 180° = 0.
5. Вывести основное тригонометрическое тождество sin2 + cos2 = 1, используя рисунок 290.
III. Закрепление изученного материала (решение задач).
1. Решить задачи № 1012 (для точек А, В, М1, М2).
2. Решить задачи № 1013 (б) на доске и в тетрадях.
Дано: cos =![]() .
.
Найти: sin .
Решени.
sin2 + cos2 = 1; sin2 = 1 – cos2 ; sin =![]() .
.
sin =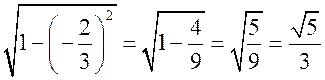 .
.
Ответ: ![]() .
.
3. Решить задачи № 1014 (а) и № 1015 (г).
решение
г) sin = ![]() и 90° < < 180°. Угол расположен во II четверти, значит, cos < 0. Найдем cos , используя основное тригонометрическое тождество:
и 90° < < 180°. Угол расположен во II четверти, значит, cos < 0. Найдем cos , используя основное тригонометрическое тождество:
cos2 = 1 – sin2
cos = 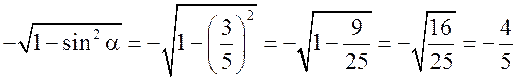 ;
;
найдем tg .
tg = 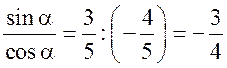 .
.
Ответ: ![]() .
.
IV. Итоги урока.
Домашнее задание: изучить материал пунктов 93 и 94; ответить на вопросы 1–4, с. 271; решить задачи № 1012 (для точек М2 и М3), №№ 1013 (б, в), 1014 (б, в), 1015 (б).