Поурочные разработки по геометрии 9 класс
Уравнение окружности. Решение задач - МЕТОД КООРДИНАТ
Цели: закрепить знания учащихся в ходе решения задач; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Результаты математического диктанта. Указать ошибки, сделанные учащимися.
2. На доске один ученик выводит уравнение окружности.
3. С остальными учащимися проверяется решение домашних задач.
II. Выполнение упражнений.
1. Решить задачу.
Напишите уравнение окружности с центром в точке А (0; 4), проходящей через точку D (–6; –4).
Решение
Центр окружности имеет координаты А (0; 4). Найдем радиус окружности r = AD по формуле: d =![]() .
.
r = AD =![]() = 10; r = 10.
= 10; r = 10.
Значит, искомое уравнение окружности имеет вид: (x – 0)2 + (y – 4)2 = 102; x2 + (y – 4)2 = 100.
Ответ: x2 + (y – 4)2 = 100.
2. Решить задачу № 969 (а) на доске и в тетрадях.
Решение
Диаметр окружности MN =![]() = 2
= 2![]() ; найдем радиус окружности r =
; найдем радиус окружности r = ![]() . Координаты центра окружности найдем, используя формулы для нахождения координат середины отрезка MN: x =
. Координаты центра окружности найдем, используя формулы для нахождения координат середины отрезка MN: x =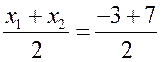 = 2; y =
= 2; y =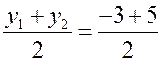 = 1. Центр В (2; 1). Напишем уравнение окружности: (x – 2)2 + (y – 1)2 = 41.
= 1. Центр В (2; 1). Напишем уравнение окружности: (x – 2)2 + (y – 1)2 = 41.
3. Решить задачу № 970.
Решение
Центр окружности лежит на оси абсцисс, то координаты центра D (x; 0); радиус равен r = 5. Окружность проходит через точку А (1; 3), тогда AD = r, поэтому (x – 1)2 + (3 – 0)2 = r2 = 52, (x – 1)2 + 9 = 25;
x2 – 2x – 15 = 0; x1 = –3; x2 = 5.
Следовательно, координаты центров окружностей D1 (–3; 0) и D2 (5; 0). Существует две таких окружности: (x + 3)2 + y2 = 25 и (x – 5)2 + y2 = 25.
4. Решить задачу № 971 на доске и в тетрадях.
Решение
Центр окружности лежит на оси ординат, значит, координаты центра С (0; y). По условию, окружность проходит через точки А (–3; 0) и В (0; 9), значит, расстояния АС = ВС = r радиусу:
(0 + 3)2 + (y – 0)2 = (0 – 0)2 + (y – 9)2;
9 + y2 = y2 – 18y + 81; 18y = 72; y = 4.
Следовательно, центр окружности имеет координаты С (0; 4).
Найдем радиус окружности: r2 = AC2 = (0 + 3)2 + (4 – 0)2 = 9 + 16 = 25; r = 5. Напишем уравнение окружности: (x – 0)2 + (y – 4)2 = 52; то есть x2 + (y – 4)2 = 25.
5. Решить задачу № 1002(а) на доске и в тетрадях (решение задачи объясняет учитель).
Решение
Координаты точек А, В и С должны удовлетворять уравнению окружности (x – a)2 + (y – b)2 = r2.
Подставив в это уравнение координаты данных точек, получим систему трех уравнений относительно неизвестных a, b и r :
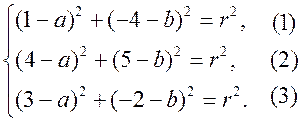
Вычтем из уравнения (1) сначала уравнение (2), а затем уравнение (3). Получим систему двух линейных уравнений с неизвестными a и b, которую учащиеся могут решить самостоятельно 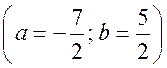 . Подставив эти значения в любое из уравнений, например, в уравнение (1), находим значение r2 и записываем искомое уравнение:
. Подставив эти значения в любое из уравнений, например, в уравнение (1), находим значение r2 и записываем искомое уравнение: 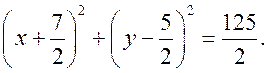
III. Итоги урока.
Домашнее задание: повторить материал пунктов 86–91; решить задачи №№ 969 (б), 981 (есть решение в учебнике), 1002 (б).