Уроки-конспекты по Геометрии 8 класс
ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ - урок 5
Цель: рассмотреть свойства и признаки равнобокой трапеции при решении задач.
Ход урока
I. Проверка домашнего задания.
1. Ответить на вопросы учащихся по домашнему заданию.
2. Выполнить задание (устно).
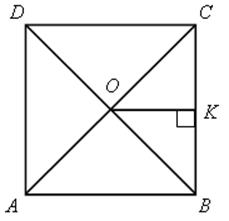
АВСD – квадрат.
Вид четырехугольника АОKВ определить.
Найти его углы.
Решение
![]() ОАВ = 45° по свойству квадрата,
ОАВ = 45° по свойству квадрата,
![]() АОK = 180° – 45° = 135°,
АОK = 180° – 45° = 135°,
![]() ОKВ =
ОKВ = ![]() KВА = 90°.
KВА = 90°.
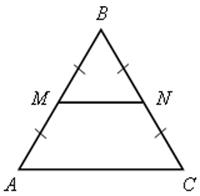
3. ![]() АВС – равносторонний. Определить вид четырехугольника МNCA.
АВС – равносторонний. Определить вид четырехугольника МNCA.
Найти его углы.
Решение
![]() А =
А = ![]() С = 60°,
С = 60°,
![]() М =
М = ![]() N = 180° – 60° = 120°.
N = 180° – 60° = 120°.
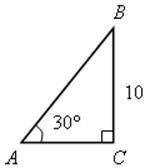
4. АВ – ?
II. Решение задач.
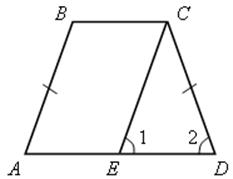
№ 388 (а). План решения.
I способ:
1) Проведем СЕ || АВ.
2) Докажем, что АВСЕ – параллелограмм, тогда АВ = СЕ.
3) Докажем, что ![]() СDЕ – равнобедренный, тогда
СDЕ – равнобедренный, тогда ![]() 1 =
1 = ![]() 2.
2.
4) Докажем, что ![]() А =
А = ![]() 2. (Используя, что АВ || CЕ,
2. (Используя, что АВ || CЕ, ![]() А и
А и ![]() 1 – соответственные.)
1 – соответственные.)
5) Докажем, что ![]() В =
В = ![]() ВСD (используя, что АD || ВС,
ВСD (используя, что АD || ВС, ![]() В и
В и ![]() А,
А, ![]() ВСD и
ВСD и ![]() 2 – пары внутренних односторонних углов).
2 – пары внутренних односторонних углов).
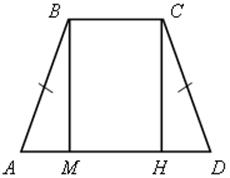
II способ:
1) Проведем ВМ ![]() АD и СН
АD и СН ![]() АD.
АD.
2) Докажем, что ВСНМ – параллелограмм, тогда ВМ = ЕН.
3) Докажем, что ![]() АВМ =
АВМ = ![]() DСН (по катету и гипотенузе), тогда
DСН (по катету и гипотенузе), тогда ![]() А =
А = ![]() D.
D.
4) Аналогично I способу докажем, что ![]() АВС =
АВС = ![]() ВСD.
ВСD.
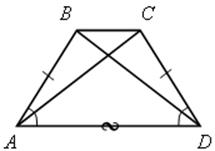
№ 388 (б) – устно.
![]() А =
А = ![]() D по свойству равнобокой трапеции АВ = СD.
D по свойству равнобокой трапеции АВ = СD.
АD – общая.
![]() АВD =
АВD = ![]() DСА по I признаку равенства треугольников, тогда АС = ВD.
DСА по I признаку равенства треугольников, тогда АС = ВD.
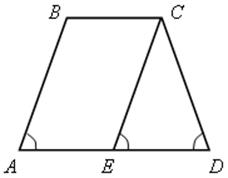
№ 389 (признаки равнобокой трапеции; обратная теорема № 388 (а; б).
а) Проведем СЕ || АВ, тогда ![]() А =
А = ![]() Е =
Е = ![]() D.
D.
![]() СЕD – равнобедренный, поэтому СD = СЕ, а так как АВСZ – параллелограмм, то АВ = СЕ. Имеем АВ = СЕ = СD.
СЕD – равнобедренный, поэтому СD = СЕ, а так как АВСZ – параллелограмм, то АВ = СЕ. Имеем АВ = СЕ = СD.
АВСD – равнобокая трапеция.
б) ![]() АСD =
АСD = ![]() DВА по I признаку равенства треугольников, тогда АВ = СD.
DВА по I признаку равенства треугольников, тогда АВ = СD.
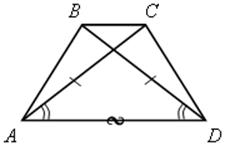
№ 389. Можно решить устно (если класс является более подготовленным).
№ 390 (устно).
III. Самостоятельная работа.
Вариант I
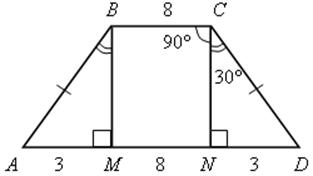
Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.
Вариант II
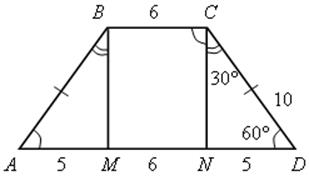
Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60°.
Вариант III
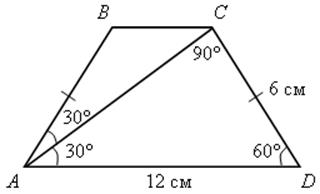
Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если основание АD равно 12 см, а угол АDС равен 60°.
Проверить самостоятельную работу можно на этом же уроке с помощью закрытой доски (устно):
Вариант I
СD = 2ND = 6 см.
Вариант II
ND = ![]() CD = 5 см.
CD = 5 см.
Вариант III
СD = ![]() АD = 6 см.
АD = 6 см.
ВС = 6 см.
IV. Итоги урока.
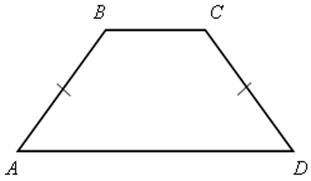
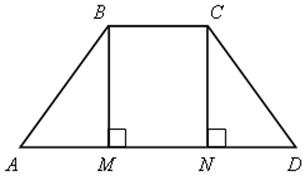
Свойства равнобокой трапеции.
АВСD – равнобокая трапеция |
|
1) 2) АС = ВD 3) |
Признаки равнобокой трапеции. АВСD – трапеция.
|
|
АВСD – равнобокая трапеция |
АС = ВD |
|
АВСD – равнобокая трапеция |
Домашнее задание: вопросы 10, 11, с. 114–115; №№ 392 (а, б), 438; повторить § 4 и № 222, п. 38, задача 1; принести циркуль.
Для желающих.
В равнобокой трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой – полуразности оснований.
