ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ТРЕУГОЛЬНИКА И ТРАПЕЦИИ - урок 5

Цель: познакомить учащихся с методами решения задач по теме «Площадь многоугольников».

Ход урока

I. Проверка домашнего задания.

1. Обсудить решение домашних задач.

2. Выполнить задания (устно):

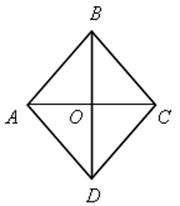
1) АВСD – ромб.

ВD = 18 см, АС = 10 см.

Найти: SАВСD.

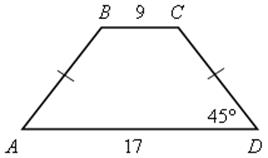
2) АВСD – равнобокая трапеция.

Найти: SАВСD.

II. Решение задач.

№ 477.

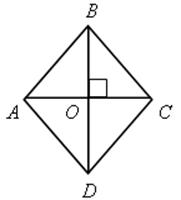
Решение

Пусть АС = х, тогда ВD = 1,5х,

SАВСD = АС · ВD,

27 = x ∙ x; 27 = x2.

х2 = 36; х = 6.

АС = 6 см, ВD = 9 см.

№ 478.

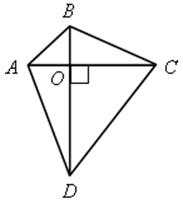
Решение

1) SАВСD = SАВС + SАDС.

2) ВО – высота АВС, а DО высота АDС, поэтому SАВС = АС · ВО, SАDС = АС · ОD.

Следовательно SАВСD = АС · ВО + АС · ОD = АС (ВО + ОD); SАВСD = АС · ВD.

Задача 1. В трапеции АВСD АD – большее основание, D = 60. Биссектрисы углов С и D пересекаются в точке О, ОD = а, ВС = b, АD = с. Найдите площадь трапеции.

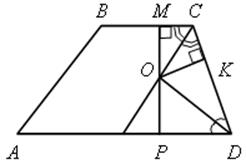
Решение

1) Проведем ОМ ВС, ОK СD и ОР АD.

2) Из равенства прямоугольных треугольников МСО и KСО следует, что ОМ = ОK.

3) Из равенства прямоугольных треугольников ОРD и ОKD следует, что ОK = ОР.

4) Имеем ОМ = ОР = ОK.

5) В прямоугольном треугольнике KОD катет ОK лежит против угла в 30 и равен половине гипотенузы, то есть ОK = .

6) SАВСD = (ВС · АD) · МР; SАВСD = (b + с).

Задача 2. Четырехугольник, у которого диагонали пересекаются под прямым углом, имеет площадь 250 см2. Найдите его диагонали, если известно, что одна больше другой в 5 раз.

Ответ: 10 и 50 см.

III. Итоги урока.

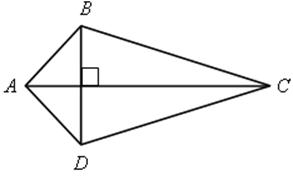
SАВСD = d1 · d2 – площадь четырехугольника, где d1 и d2 – диагонали.

Домашнее задание: вопросы 1–7, с. 133–134; №№ 476 (б), 470, 466.