itle

Во второй главе изучаются признаки равенства треугольников. Они являются основным рабочим аппаратом всего курса геометрии. Доказательства большей части теорем курса строятся по схеме: поиск равных треугольников — доказательство их равенства — следствия, вытекающие из равенства треугольников. Признаки равенства треугольников открывают широкие возможности для решения задач и, таким образом, позволяют накапливать опыт доказательных рас- суждений. Доказательства первого и второго признаков состоят в том, что один треугольник совмещается с другим путем наложения, а это означает, что треугольники равны по определению равенства фигур. Этот приём нагляден, понятен учащимся, вполне соответствует их представлениям о равенстве фигур.

На начальном этапе изучения признаков равенства треугольников полезно больше внимания уделять решению задач по готовым чертежам, применяя таблицы и ТСО. В дальнейшем при решении задач данной главы нужно нацеливать учащихся на самостоятельное выполнение рисунка по условию задачи, что во многих случаях помогает быстрее найти и применить подходящий признак равенства треугольников.

Второй важный момент данной главы - введение нового класса задач - на построение с помощью циркуля и линейки.

Урок 1. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (§ 1) (3 часа)

Цели: ввести понятия треугольника и его элементов, периметра треугольника; учить оформлять и решать задачи; развивать логическое мышление учащихся.

Оборудование: различные многоугольники и треугольники, вырезанные из бумаги или изготовленные из проволоки; таблицы «Виды треугольников» и «Равенство треугольников».

Ход урока

I. Анализ контрольной работы.

1. Сообщение итогов контрольной работы.

2. Ошибки, допущенные учащимися в ходе работы.

3. Решение на доске задач, вызвавших затруднения у учащихся.

II. Изучение нового материала методом беседы.

1. Понятие треугольника знакомо учащимся, поэтому изучение темы начинается с демонстрации различных многоугольников, треугольников, изготовленных из бумаги, проволоки либо изображенных на таблице или классной доске.

2. Учащиеся выделяют треугольники, указывают и называют их стороны, вершины и углы. Обозначение треугольника, его углов, сторон.

3. Выполнение практического задания:

1) Начертите треугольник ABC и проведите отрезок, соединяющий вершину А с серединой противоположной стороны.

2) Начертите треугольник MNP. На стороне МР отметьте произвольную точку К и соедините ее с вершиной, противолежащей стороне МР.

3) Назовите углы: а) треугольника ДЕК, прилежащие к стороне ЕК; б) треугольника MNP, прилежащие к стороне MN.

4) Назовите угол: а) треугольника ДЕК, заключенный между сторонами ДЕ и ДК; б) треугольника MNP, заключенный между сторонами NP и РМ.

5) Между какими сторонами: а) треугольника ДЕК заключен угол К, б) треугольника MNP заключен угол N?

4. Выполнение заданий № 87 и 88 для лучшего усвоения понятий треугольника и его элементов.

5. Введение понятия периметра треугольника. Записать в тетради: сумма длин трех сторон треугольника называется его периметром.

6. Решение задачи № 91 с оформлением на доске и в тетрадях учащихся:

Дано: РΔАВС = 48 см, АС = 18 см, ВС - АВ = 4,6 см.

Найти: АВ и ВС.

Решение:

Обозначим длину стороны АВ в сантиметрах буквой х, тогда ВС = (х + 4,6) см;

48 см = АВ + АС + ВС = х + х + 4,6 + 18 см, откуда 2х - 25,4; х = 12,7.

Значит, АВ = 12,7 см; ВС = 12,7 + 4,6 + 17,3 (см).

Ответ: 12,7 см и 17,3 см.

7. Вспомнить, какие фигуры называются равными. Записать в тетрадях определение:

Два треугольника называются равными, если каждой стороне и каждому углу в любом из них найдется равный элемент в другом.

8. Работа по рис. 50 и таблице «Равенство треугольников».

Обратить внимание учащихся на то, что из равенства треугольников следует равенство соответствующих, то есть совмещающихся при наложении сторон и углов этих треугольников, и что в равных треугольниках против соответственно равных сторон лежат равные углы и обратно, против соответственно равных углов лежат равные стороны.

9. Устно решить задание: на каждом из рисунков 1 и 2 изображены равные между собой треугольники. Указать соответственно равные элементы этих треугольников.

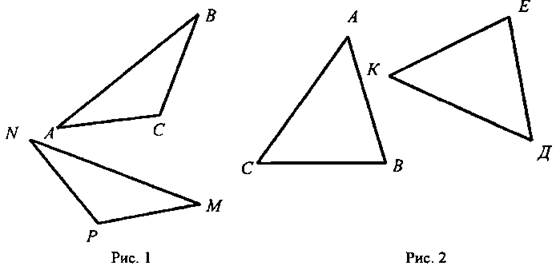
10. Устное решение задачи № 92.

11. Письменно решить задачу:

Треугольники ABC и MNP равны, причем ∠A = ∠M, ∠B = ∠N и ∠C = ∠P. Найдите стороны ΔМNР, если АВ = 7 см, ВС = 5 см, СА = 3 см.

Решение:

ΔABC = ΔМNP по условию, поэтому углы и стороны ΔABC соответственно равны углам и сторонам треугольника MNP. Из условия задачи следует, что соответственно равными являются стороны АВ и MN, ВС и NP, СА и РМ.

Значит, MN = 7 см, NP = 5 см, РМ = 3 см.

III. Закрепление изученного материала.

1. Учащиеся самостоятельно выполняют практическое задание № 89 (б; в).

Учитель просматривает выполнение этого задания и устраняет ошибки.

2. Решение задачи № 90 (самостоятельно).

IV. Итоги урока.

Используя таблицы, учитель с помощью вопросов выясняет, умеют ли учащиеся объяснить, какая фигура называется треугольником, и назвать его элементы; знают ли, что такое периметр треугольника, какие треугольники называются равными.

Домашнее задание: изучить п. 14 из § 1; ответить на вопросы 1 и 2 на с. 49; решить задачу № 156; выполнить практическое задание 89 (а).