itle

Цели: рассмотреть свойства параллельных прямых; добиться от учащихся понимания того, что накрест лежащие, соответственные и односторонние углы можно рассмотреть для любых двух прямых и секущей, но только в случае параллельных прямых накрест лежащие углы равны, соответственные углы равны, а сумма односторонних углов составляет 180°.

Ход урока

I. Проверка усвоения материала учащимися.

1. Сформулировать определение параллельных прямых.

2. Повторить признаки параллельности двух прямых.

3. Сформулировать аксиому параллельных прямых.

4. Повторить следствия из аксиомы параллельных прямых.

5. Устно решить задачу: докажите, что прямая, параллельная основанию АС равнобедренного треугольника ABC, перпендикулярна прямой ВД, где ВД - медиана треугольника.

II. Объяснение нового материала.

1. Во всякой теореме различают две части: условие и заключение. Условие теоремы — это то, что дано, а заключение - то, что требуется доказать.

2. Привести примеры изученных теорем и выделить в них условие и заключение (это делают учащиеся).

3. Ввести понятие теоремы, обратной данной.

4. Сформулировать теоремы, обратные трём теоремам п. 25, выражающим признаки параллельности прямых. Необходимо сравнить условия и заключения двух теорем: теоремы, выражающей признак параллельности двух прямых, и обратной, составив следующую таблицу:

Признак параллельности прямых а и в	Свойство параллельных прямых а и в
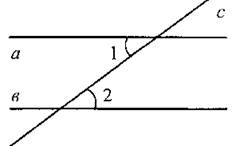
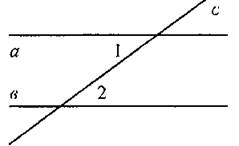
Дано: прямые а и в, секущая с, ∠1 и ∠2 - накрест лежащие углы; ∠1 = ∠2. Доказать: а || в.	Дано: прямые а и в, секущая с, ∠1 и ∠2 - накрест лежащие углы; а || в. Доказать: ∠1 = ∠2.

5. Рассмотреть доказательство теоремы о накрест лежащих углах по рисунку 113 и таблице.

6. Акцентировать внимание учащихся на методе доказательства от противного, с помощью которого и была доказана теорема. Кроме того, важно отметить, что если верно некоторое утверждение, то отсюда еще не следует, что и обратное утверждение тоже верно. Например, рассмотрим два утверждения:

1) Если точка С - середина отрезка АВ, то АС = ВС.

2) Если АС = ВС, то точка С - середина отрезка АВ. Второе утверждение является обратным первому. Первое утверждение верно, в то время как второе неверно. В самом деле, в равнобедренном треугольнике ABC с основанием АВ отрезки АС и ВС равны, но точка С не является серединой отрезка АВ.

7. Самостоятельно по учебнику учащиеся изучают теоремы о свойствах соответственных и односторонних углов, образованных двумя параллельными и секущей.

III. Закрепление изученного материала.

1. Устно по рисунку 114 учебника доказать следствие: если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

2. Устно решить № 201, 205 по рисунку 117 и № 209 по рисунку 118.

IV. Итоги урока.

Домашнее задание: изучить п. 29; повторить пункты 15-28; ответить на вопросы 1—15 на с. 68 учебника; решить задачи № 202 и 212.