Поурочные разработки по Геометрии 11 класс
Повторение по теме: «Комбинации с вписанными сферами» - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цели урока:
- систематизировать теоретические знания о комбинациях тел;
- научить учащихся решать задачи на комбинации с вписанными сферами.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
Проверка домашнего задания.
Задача № 748 (рис. 1).
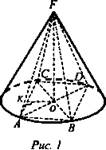
Решение: ![]() Из ΔАОК по определению синуса угла
Из ΔАОК по определению синуса угла ![]()
![]() - радиус основания конуса,
- радиус основания конуса, ![]()
![]()
![]() Из ΔFОК по определению котангенса угла
Из ΔFОК по определению котангенса угла ![]()
![]()
 (Ответ:
(Ответ: ![]() )
)
Задача № 749 (рис. 2).
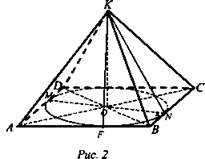
Решение: ![]()
![]()
![]()
![]() Из ΔKON по определению тангенса
Из ΔKON по определению тангенса ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Пока идет проверка домашнего задания провести индивидуальную работу по карточкам (см. приложение).
Ответы:
I уровень: 24R2; 8R3.
II уровень: 100π; 500π/3.
III уровень: 36п; 36π.
Решение карточек
Карточка 1
Дано: шар вписан в параллелепипед, OO1 = R (рис. 3).
Найти: Sполн.
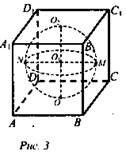
Решение: Так как шар вписан, то OO2 = MN, значит ABCDA1B1C1D1 - куб. АВ = 2R, тогда ![]() (Ответ: 24R2.)
(Ответ: 24R2.)
Карточка 2
Дано: шар вписан в призму, АВ = ВС, O1М = R (рис. 4).
Найти: Vпризмы.
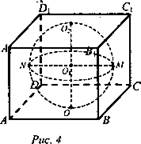
Решение: Так как шар вписан в призму, то эта призма будет являться кубом со стороной 2R. ![]() (Ответ: 8R3.)
(Ответ: 8R3.)
Карточка 3
Дано: АВСА1В1С1 - призма, ∠ACB = 90°, АВ = 25, С1Н = 12, сфера вписана в призму (рис. 5).
Найти: Scферы.
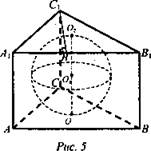
Решение: ![]() по свойству высоты, проведенной из вершины прямого угл.
по свойству высоты, проведенной из вершины прямого угл.
![]()
![]() или
или ![]() Тогда НВ1 = 16 или НВ1 = 9. Найдем радиус окружности, вписанной в ΔА1В1С1, который будет являться радиусом сферы.
Тогда НВ1 = 16 или НВ1 = 9. Найдем радиус окружности, вписанной в ΔА1В1С1, который будет являться радиусом сферы. ![]() Из ΔC1HB1 по теореме Пифагора
Из ΔC1HB1 по теореме Пифагора ![]()
![]() из ΔА1С1H:
из ΔА1С1H: ![]()
![]()
![]() Найдем Scферы.
Найдем Scферы. ![]()
![]() (Ответ: 100π.)
(Ответ: 100π.)
Карточка 4
Дано: шар вписан в прямую призму, ∠ACB = 90°, АС = 15 см, А1Н = 9 см (рис. 6).
Найти: Vшара.
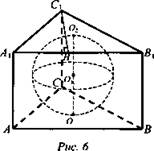
Решение: Из ΔА1С1Н по теореме Пифагора ![]()
![]() по свойству высоты, проведенной из вершины прямого угла,
по свойству высоты, проведенной из вершины прямого угла, ![]() тогда
тогда
Найдем радиус окружности, вписанной в ΔА1В1С1, который будет являться радиусом сферы ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Карточка 5
Дано: шар вписан в прямую призму, ABCD - трапеция, ∠ABC = ∠BAD = 90°, ВС = 4 см, AD = 12 см (рис. 7).
Найти: Scферы.
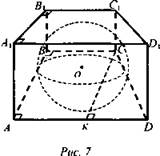
Решение: Найдем радиус окружности, вписанной в трапецию ABCD, который будет являться радиусом сферы. Пусть АВ = х, тогда СК = х, KD = AD - AK, KD = 12 - 4 = 8 (см). Из ΔCKD по теореме Пифагора найдем CD: ![]() Так как в трапецию вписана окружность, то АВ + CD = AD + ВС. Составим и решим уравнение
Так как в трапецию вписана окружность, то АВ + CD = AD + ВС. Составим и решим уравнение ![]() уравнение равносильно системе:
уравнение равносильно системе: ![]()
![]() Значит, АВ = 6, но АВ - диаметр вписанной окружности, следовательно,
Значит, АВ = 6, но АВ - диаметр вписанной окружности, следовательно, ![]() (Ответ: 36π см2.)
(Ответ: 36π см2.)
Карточка 6
Дано: шар вписан в прямую призму, ABCD - трапеция, AB = CD, ВС = 2 см, AD = 18 см (рис. 8).
Найти: Scферы.
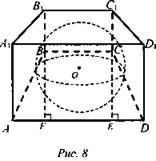
Решение: Опустим из вершин В и С перпендикуляры к AD. FE = 2 см, тогда AF = ED = 8 см. Так как окружность вписана в трапецию (ее радиус будет равен радиусу сферы), то АВ + CD = AD + ВС, но AB = CD, 2АВ = 2 + 18, АВ = 10 см. По теореме Пифагора из ΔABF найдем BF: ![]() BF - диаметр, значит r = 3 см. Найдем Scферы.
BF - диаметр, значит r = 3 см. Найдем Scферы. ![]()
![]() (Ответ: 36π.)
(Ответ: 36π.)
III. Самостоятельное решение задач
Задача № 750 (рис. 9).
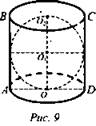
Решение: пусть AO = R, тогда АВ = 2R. ![]()
![]()
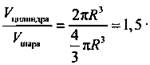 (Ответ: 1,5.)
(Ответ: 1,5.)
Задача № 752 (рис. 10).
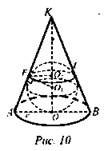
Решение: из ΔАОК по теореме Пифагора ![]()
![]() AF = AO - как отрезки касательных, проведенных из одной точки. ΔAKO ~ ΔFKO2 (∠AOK = ∠O1FK = 90°. ∠AKO - общий) по первому признаку подобия треугольников. Из подобия треугольников следует
AF = AO - как отрезки касательных, проведенных из одной точки. ΔAKO ~ ΔFKO2 (∠AOK = ∠O1FK = 90°. ∠AKO - общий) по первому признаку подобия треугольников. Из подобия треугольников следует ![]()
![]() Найдем длину l1 линии, по которой сфера касается конуса.
Найдем длину l1 линии, по которой сфера касается конуса.
![]() (Ответ:
(Ответ: ![]() )
)
Наводящий вопро.
- Почему ∠KFO1 = 90°.
Задача № 753 (рис. 11).
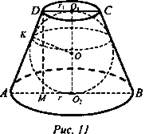
Решение: S = πr2 - площадь нижнего основания, S1 = πr12 - площадь верхнего основания. AO2 = AK = r, DO1 = DK = r1 - как отрезки касательных, проведенных из одной точки. Тогда AD = r + r1, АМ = АO2 - МO2 = АO2 – DO1 = r – r1. Из ΔAMD по теореме Пифагора ![]() тогда
тогда ![]() Найдем отношение объема усеченного конуса к объему шара.
Найдем отношение объема усеченного конуса к объему шара. 
![]() (Ответ:
(Ответ: ![]() )
)
Дополнительная задача (относится к третьему уровню).
В полушар вписан цилиндр, причем одно из оснований цилиндра лежит в плоскости диаметрального круга полушара, а высота цилиндра вдвое меньше радиуса полушара. Найдите отношение объема цилиндра к объему полушара.
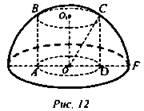
Решение: пусть OF = 2R, тогда CD = R. Из ΔOCD по теореме Пифагора найдем OD,
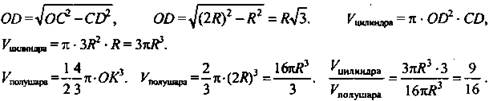
(Ответ: 9/16.)
IV. Подведение итогов года