Поурочные разработки по Геометрии 11 класс
Объем шара - урок 2 - Объем шара и площадь сферы - ОБЪЕМЫ ТЕЛ
Цель урока:
- совершенствовать навыки решения задач на применение формул для вычисления объема шара.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
Три ученика вызываются к доске и получают задания:
а) вывести формулу для вычисления объема шара;
б) кратко записать решение домашнего задания № 710 а), б), 711;
в) краткое решение № 713.
Задача № 710 а). Дано: R = 4 см. ![]()
Найти: V и S.
Решение. ![]() (Ответ:
(Ответ: ![]() )
)
Задача № 710 б). Дано: V = 113,04 см3.
Найти: S.
Решение. ![]()
![]() (Ответ: 36π см2.)
(Ответ: 36π см2.)
Задача № 711.
Решение: ![]()
![]() если
если ![]() то
то ![]() (Ответ: в 4 раза.)
(Ответ: в 4 раза.)
Задача № 713.
Решение: h= 12 см, r = 5/2 = 2,5 см. ![]()
![]() (Ответ: 125/6π см3.)
(Ответ: 125/6π см3.)
Надо сравнить объемы конуса и шара: 25π и 125/6π, 150 и 125. Так как 150 > 125, то 25π > 125π/6, Vк > Vш., то есть растаявшее мороженое уместится в стаканчике.
Пока ученики готовятся у доски, остальным учащимся предлагается ответить на вопросы математического диктанта через копирку. Предлагается два варианта.
Математический диктант.
1. Вычислите объем шара, если его радиус R = 6 см. [R = 5 см].
2. Вычислите диаметр шара, если его объем V = 36π. [V= 32π/3].
3. Объем шара равен 256π/3 см3. [288π см3]. Найдите площадь большего круга [длину окружности большего круга].
4. В цилиндр вписан шар радиуса R = 1 [R = 2]. Найдите отношение Vцил. : Vшара [Vшара : Vцил.].
5. Для вычисления объема шара ученик предложил свою формулу ![]()
Какие он должен дать пояснения, подтверждающие правильность этой формулы?
Ответы к математическому диктанту:
Вариант I 1. 228π; 2. 3; 3. 16π; 4. ![]()
Вариант II 1. 500π/3; 2. 2; 3. 12π; 4. ![]()
Проверяются ответы на вопросы диктанта, слушается доказательство, проверяется домашнее задание.
III. Формирование умения и навыков учащихся
1. Разобрать и решить задачу. Один из учащихся решает задачу у доски, остальные в тетрадях. Учитель контролирует правильность решения, при необходимости задает наводящие вопросы.
Задача. Сторона основания правильной четырехугольной пирамиды равна 10√3, а угол боковой грани с плоскостью основания равен 60°. Найдите объем шара, вписанного в пирамиду (рис. 1).
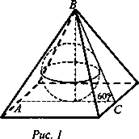
Решение: Рассмотрим сечение, проведение через высоту пирамиды и две апофемы. В сечении получается ΔАВС - равносторонний. Радиус вписанной в него окружности будет равен ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
2. Подробно разбирается решение задачи у доски и записывается учениками в тетрадях.
Задача. В шар вписана правильная треугольная призма так, что ее высота вдвое больше стороны основания. Найдите объем шара, если объем призмы равен 27/π (рис. 2).

Решение:
1) Пусть х - сторона основания. Тогда высота призмы 2х. Ее объем V = Sосн. · h. ![]() По условию
По условию ![]()
![]()
2) Радиус R найдем из ΔOO1A1. O1A1 - радиус описанной окружности около треугольника A1B1C1. ![]()
![]() , так как О - середина О1О2.
, так как О - середина О1О2.
![]()
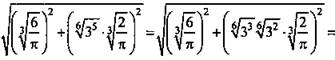
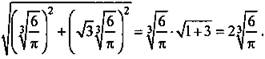 Объем шара
Объем шара ![]()
![]() (Ответ: V = 64.)
(Ответ: V = 64.)
3. Один ученик решает задачу у доски, остальные записывают решение в тетрадях.
Задача. В конус, осевое сечение которого равносторонний треугольник, вписан шар. Найти объем шара, если объем конуса равен 27 (рис. 3).
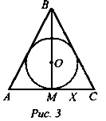
Решение: В осевом сечении комбинации тел получим равносторонний треугольник (по условию) и вписанный в него круг.
Радиус шара равен радиусу круга, а диаметр основания конуса равен стороне АС треугольника. Пусть х - радиус основания конуса. Тогда АС = 2х, высота BM = x√3 (из ΔВMС). Объем конуса V = 27. ![]() (Ответ:
(Ответ: ![]() )
)
Радиус окружности, вписанной в треугольник, найдем по формуле ![]() Наконец, объем шара
Наконец, объем шара ![]() (Ответ: V = 12.)
(Ответ: V = 12.)
IV. Подведение итогов
- Назовите форму для вычисления объема шара.
Оценить работу учащихся на уроке.
Домашнее задание
Вопрос № 11 (стр. 161), № 753, 754.
Дополнительные задачи.
I уровень
Внешний диаметр полого шара 18 см, толщина стены 3 см. Найдите объем материала, из которого изготовлен шар.
Решение: ![]()
![]() (Ответ: 684π см3.)
(Ответ: 684π см3.)
II уровень
Диаметр свинцового шара равен 30 см.
Сколько шариков, диаметр которых 3 см, можно сделать из этого свинца?
Решение: ![]()
![]()