Поурочные разработки по Геометрии 11 класс
Объем пирамиды - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ
Цель урока:
- вывести формулу объема пирамиды с использованием основной формулы объема тел.
Ход урока
I. Объяснение нового материала (п. 69.)
Докажем теорему:
Объем пирамиды равен одной трети, произведения площади основания на высоту.
![]()
Доказательство:
Сначала докажем теорему для треугольной пирамиды, затем для произвольной.
1. Рассмотрим треугольную пирамиду ОАВС с объемом V, площадью основания S и высотой h (рис. 1). Проведем ось ох (ОМ2 - высота), рассмотрим сечение A1B1C1 пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1 пересечения этой плоскости с осью ох, а через S(x) - площадь сечения. Выразим S(x) через S, h и х. Заметим, что ΔA1B1C1 ∞ ABC.
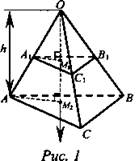
В самом деле A1B1 || AB, тогда ΔOA1B1 ∞ ΔOAB, следовательно, ![]()
Прямоугольные треугольники ОА1М1 и ОАМ2 тоже подобны (они имеют общий острый угол с вершиной О). Поэтому ![]()
Таким образом, ![]()
Аналогично доказывается ![]()
Итак, ΔA1B1C1 ∞ ABC, h = x/h, следовательно, ![]()
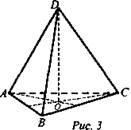
Применим теперь основную формулу для вычисления объемов тел при а = 0, b = h, получаем
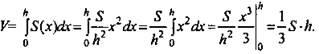
2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S (рис. 2). Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h. Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель 1/3h, получим в скобках сумму площадей оснований треугольных пирамид, т.е. площадь S основания исходной пирамиды. Таким образом, объем исходной пирамиды равен 1/3Sh. Теорема доказана.
II. Решение задач (по готовым чертежам)
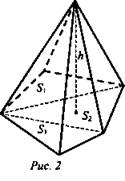
Дано: ABCD - правильная пирамида. АВ = 3; AD = 2√3 (рис. 3).
Найти: a) Socн.; б) АО; в) DO; г) V.
Решение:
а) ![]() (используем формулу для вычисления площади правильного треугольника).
(используем формулу для вычисления площади правильного треугольника). ![]()
б) ![]() (формула радиуса описанной окружности через сторону правильного треугольника).
(формула радиуса описанной окружности через сторону правильного треугольника). ![]()
в) ![]() (по теореме Пифагора).
(по теореме Пифагора). 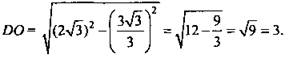
г) ![]()
(Ответ: ![]() )
)
2. Дано: ABCDF - правильная пирамида. ∠FCO = 45°; FO = 2 (рис. 4).
Найти: a) Socн.; б) V.
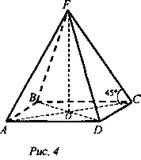
Решение:
1) Рассмотрим ΔFOC: ∠O = 90°, ∠C = 45°, значит, ∠F = 45°. Следовательно, ΔFOC - равнобедренный, ОС ≈ FO = 2.
2) АС = 2OС = 4. d = AC = AD√2 (по свойству диагонали квадрата, d2 = 2а2). Тогда ![]()
3) ABCD - квадрат (пирамида правильная). ![]()
4) ![]()
(Ответ: a) 8; 6) 5·1/3.)
3. Дано: ABCDEKF - правильная пирамида. FO ⊥ (ABC), FM ⊥ AK, FO = 4, FM = 5 (рис. 5).
Найти: a) Socн.; б) V.
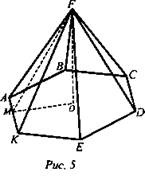
Решение:
1) Рассмотрим ΔFOM: ∠O = 90° (так как FO ⊥ (ABC), значит, FO ⊥ OM) FO = 4, FM = 5. ![]() (по теореме Пифагора),
(по теореме Пифагора), ![]() OM = r (r - радиус окружности, вписанной в правильный шестиугольник).
OM = r (r - радиус окружности, вписанной в правильный шестиугольник). ![]()
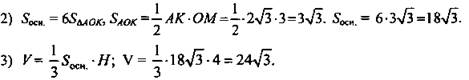
(Ответ: а) 18√3, б) 24√3.)
4. Дано: A1A2A3A4 - ромб, SA1A2A3A4 - пирамида, A1A4 = a, ∠SBO = β, ОВ ⊥ A3A4, ∠A2A1O = а (рис. 6).
Найти: V - ?
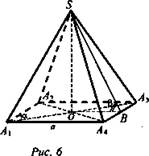
Решение:
1) Рассмотрим ![]()
![]()
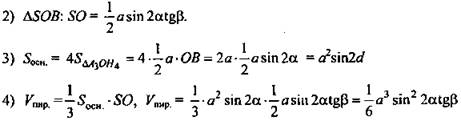
(Ответ: ![]() )
)
Домашнее задание
Вывести формулу для вычисления объема усеченной пирамиды.
П. 69, в 4,5 стр. 161. № 684 а), 686 а), 687.