Поурочные разработки по Геометрии 11 класс
Объем цилиндра - урок 2 - Объем прямой призмы и цилиндра - ОБЪЕМЫ ТЕЛ
Цели урока:
- повторить тему об объеме цилиндра;
- выработать навыки решения задач с помощью формулы объема цилиндра.
Ход урока
I. Актуализация опорных знаний
1. Доказательство теоремы об объеме цилиндра;
2. Решение задачи № 669 из домашней работы;
3. Решение задачи № 671 (г) параллельно с доской.
Задача № 669. Дано: цилиндр, Sосн. = Q, Sсеч. = S (рис. 1).
Найти: V.
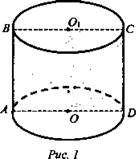
Решение: ![]()
![]()
DC = h, т.е. 
![]() (Ответ:
(Ответ: ![]() )
)
II. Формирование умений и навыков учащихся
Задача № 671 г). Дано: цилиндр, вписанная n-угольная призма, n = 8 (рис. 5 урок № 37).
Найти: ![]()
Решение: ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
III. Самостоятельная работа (20-25 мин.) (см. приложение)
Ответы:
I уровень: I вариант: № 1. 108 + 36√2 . №2. 128π: II вариант: № 1. 864√3. № 2. 54π.
II уровень: I вариант: № 1. 768√3. № 2. 3πR3; II вариант: № 1. 125. № 2. 3468π.
III уровень: I вариант: № 1. 50 см3. № 2. ![]() II вариант: № 1.4 см. № 2.
II вариант: № 1.4 см. № 2. ![]()
IV. Подведение итогов
- Какие данные необходимо иметь для определения объема цилиндра?
Собрать тетради с самостоятельными работами, сообщить правильные ответы.
Домашнее задание
П. 66, № 670, 672, 745.
Решение задач самостоятельной работы.
I уровень
Вариант I
№ 1. Дано: АВСА1В1С1 - прямая призма, ∠С = 90°, АС = 6 см, ∠ВАС = 45°, Vnp. = 108 см3 (рис. 2).
Найти: Sполн.
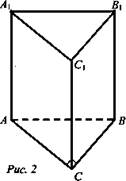
Решение:
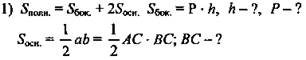
2) Рассмотрим ΔАВС - прямоугольный по условию, ∠ВАС = 45° ⇒ ΔАВС равнобедренны.
![]()
![]()
3) Найдем периметр основания: ![]()
4) Из формулы для вычисления объема прямой призмы выражаем высоту призмы и находим ее ![]()
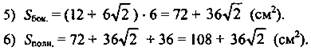
(Ответ: (108 + 36√2 см2.)
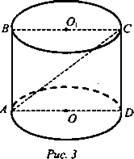
№ 2. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 8√2 см. (рис. 3).
Найдите: Vцил.
Решение:
1) ![]()
2) Рассмотрим ΔАВС - прямоугольный, так как ABCD квадрат. Пусть АВ = ВС = X см, тогда ![]()
![]() не удовлетворяет условию задачи. Итак: АВ = ВС = 8 см, т.е. h = 8 (см).
не удовлетворяет условию задачи. Итак: АВ = ВС = 8 см, т.е. h = 8 (см).
3) Найдем радиус основания: r = 1/2AD = 4 см, тогда ![]()
![]()
4) ![]()
(Ответ: 128 см3.)
Вариант II
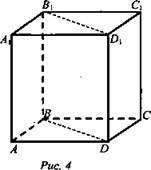
№ 1. Дано: ABCDA1B1C1D1 - прямая призма, BB1D1D - диагональное сечение, ABCD - ромб; BB1D1D - квадрат. АВ = 12 см, ∠BAD = 60° (рис. 4).
Найдите объем призмы.
Решение:
1) ![]()
2) ![]()
![]()
3) Рассмотрим ΔABD. ![]() т. е. ΔABD - равносторонний, BD = 12 cм.
т. е. ΔABD - равносторонний, BD = 12 cм.
4) Диагональное сечение BB1D1D является квадратом, т. е. h = BB1 = BD = 12 см.
5) Находим объем призмы. ![]()
(Ответ: 864√3 см3.)
№ 2. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 6√2 см (рис. 3).
Найдите: Vцил.
Решение:
1) ![]()
2) Рассмотрим ΔАВС - прямоугольный и равнобедренный, так как ABCD - квадрат. Обозначим АВ = ВС = х см, тогда ![]()
![]() не удовлетворяет условию задачи, т. е. АВ = ВС = 6 см, и так h = 6 см.
не удовлетворяет условию задачи, т. е. АВ = ВС = 6 см, и так h = 6 см.
3) Найдем радиус основания ![]()
4) ![]()
(Ответ: 54п см3.)
II уровень
Вариант I
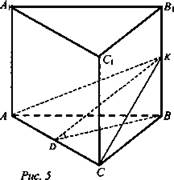
№ 1. Дано: АВСА1В1С1 - прямая призма, АВ = ВС = 10 см, АС = 12 см, К - середина ребра, ∠KDB = 60° (рис. 5).
Найти: Vпр.
Решение:
1) Рассмотрим получившееся сечение: ΔАКС и определим угол между плоскостью (АКС) и плоскостью основания. В ΔАВС проведем BD ⊥AC, тогда AC ⊥ KD (теорема о трех перпендикулярах). ∠KDB и есть линейный угол двугранного угла между плоскостью (АКС) и плоскостью основания; ∠KDB = 60°.
2) ![]()
3) Найдем площадь основания. ![]()
Рассмотрим ∠AВС: равнобедренный, поэтому BD - высота, медиана и биссектриса треугольника, т. е. AD = DC = 6 см. Далее из ∠BDC по теореме Пифагора находим высоту треугольника ABC: ![]()
![]() (Для вычисления площади ΔABC можно воспользоваться формулой Герона.)
(Для вычисления площади ΔABC можно воспользоваться формулой Герона.)
4) Найдем высоту призмы ВВ1.
Рассмотрим ΔBDK - прямоугольный, ![]()
![]()
5) ![]()
(Ответ: 768√3 см3.)
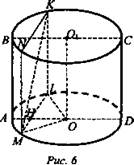
№ 2. Дано: цилиндр. (MNKL) || ОО’, ∪MAL = 120°, АО = R, ∠MKL = 30° (рис. 6).
Найти: Vцил.
Решение:
1) ![]()
2) Из ΔMOL найдем ML: ∠MOL = ∪MAL = 120°. ΔMOL - равнобедренный, проведем ОА ⊥ ML. ОА ∩ ML = Н, ОН - высота, медиана и биссектриса ΔMOL. ![]()
3) Высоту цилиндра находим из ΔMKL:![]()
![]() т. е. H = 3R.
т. е. H = 3R.
4) Находим объем цилиндра. ![]()
(Ответ: 3πR3.)
Вариант II
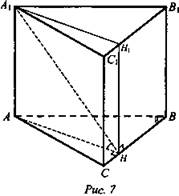
№ 1. Дано: АВСА1В1С1 - прямая призма. АВ = ВС = 10, ∠ABC = 30° (АА1Н1H) ⊥ (СС1В1В). ∠AHA1 = 45° (рис. 7).
Найти: Vnp.
Решение:
![]()
3) Рассмотрим ΔАВН: ∠AHB = 90°, ∠ABH= 30°. Найдем АН. АН = 1/2АВ (катет, лежащий против угла в 30°), АН = 5.
4) Из ΔАА1Н находим высоту призмы. h = AA1. ΔАА1Н - прямоугольный и равнобедренный, т. е. AA1 = АН = 5.
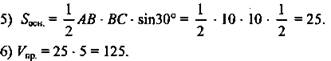
(Ответ: 125.)
№ 2. Дано: цилиндр (MNKL) || OO’, ОН = 15 см, МК = 20 см, r = 17 см (рис. 8).
Найдите: Vцил.
Решение:
1) Рассмотрим получившееся сечение: так как плоскость параллельна оси цилиндра, то MN || OO’ и KL || OO’, т.е. MN || KL; ОО’ ⊥ основанию ⇒ MN ⊥ основанию и КО ⊥ основанию, кроме того NK || ML - лежат в параллельных плоскостях, таким образом четырехугольник MNKL - прямоугольник.
2) ![]() т.е.
т.е. ![]()
3) Рассмотрим ΔMOL: проведем ОН ⊥ ML; ОН и есть расстояние от плоскости сечения до оси цилиндра, т. е. ОН = 15 см. ОН - высота, медиана и биссектриса равнобедренного ΔMOL, ![]()
![]()
4) Находим высоту цилиндра из прямоугольного ΔMKL: ![]()
![]()
5) ![]()
(Ответ: 3468π см3.)
III уровень
Вариант I
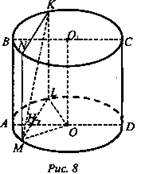
№ 1. Дано: АВСDА1В1С1D1 - прямая призма, ABCD - трапеция, SBB1C1C = 8 см2, SAA1D1D = 12 см2, BH = 5 см (рис. 9).
Найти: Vnp.
Решение:
1) Расстояние между параллельными плоскостями ВВ1С1 и AA1D1 есть длина перпендикуляра ВН, который является высотой трапеции ABCD.
2) Обозначим верхнее основание трапеции - а, нижнее - b, высоту призмы h, тогда ![]()
![]()
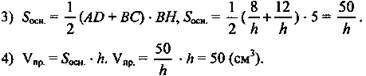
(Ответ: 50 см3.)
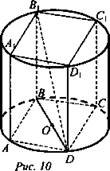
№ 2. Дано: цилиндр, АВСDА1В1С1D1 - вписанная, правильная четырехугольная призма, B1D = d, ∠DB1B = р (рис. 10).
Найти: Vцил.
Решение:
1) ![]()
2) Из прямоугольного треугольника BB1D найдем высоту цилиндра: h = ВВ1 = B1Dcosβ, h = dcosβ.
3) Sосн. = πr2. Из ΔBB1D находим катет BD, который будет являться диаметром окружности описанной около квадрата ABCD. ![]()
![]()
4) ![]()
(Ответ: ![]() .)
.)
Вариант II
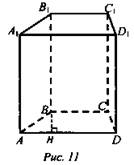
№ 1. Дано: АВСDА1В1С1D1 — прямая призма, ABCD - трапеция. Vnp. = 40 см3, SBB1C1C = 6 см2, SAA1D1D = 14 см2 (рис. 11).
Найдите: BH.
Решение:
1) Расстояние между параллельными плоскостями ВВ1С1 и AA1D1 есть длина перпендикуляра ВН, который является также высотой трапеции ABCD.
2) Обозначим: а - верхнее основание трапеции, b - нижнее основание, h - высота призмы, тогда ![]()
![]()
![]()
3) ![]()
(Oтвет: 4 см.)
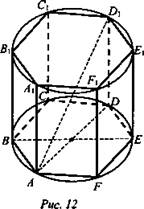
№ 2. Дано: цилиндр. АВСDEFА1В1С1D1E1F1 - правильная шестиугольная вписанная призма. AD1 = l, ∠AD1D = а (рис. 12).
Найти: Vцил.
Решение:
1) ![]()
2) Из ΔAD1D: DD1 = lcosa, т.е. h = lcosa.
3) Socн. = πr2. Из ΔAD1D находим катет AD, который является диагональю правильного шестиугольника и диаметром окружности: ![]()
4) ![]()
(Ответ: ![]() )
)