Площадь сферы - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- ознакомиться с формулой площади сферы;

- научиться решать задачи по данной теме.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихс.

1. Проверка домашнего задания

2 ученика доказывают у доски свойство и признак касательной плоскости к сфере.

а) доказательства прямой и обратной теорем о касательной плоскости;

б) решение домашних задач.

I уровень

(см. решение урок № 24).

II уровень

Задача № 591. Дано: сфера с центром в точке О касается двугранного угла в 120°, расстояние от точки О до ребра угла а (рис. 1).

Найти: АВ, R сферы.

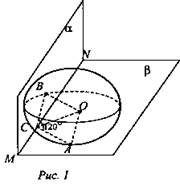
Решение: Рассмотрим сечение плоскостью, проходящей через центр шара О и перпендикулярной ребру двугранного угла MN.

Эта плоскость будет перпендикулярна и касательным к сфере плоскостями α и β. Проведем ОВ ⊥ α, ОА ⊥ β. ОВ = ОА = R.

ОА ⊥ β, AC ⊥ MN по построению, ОС ⊥ MN по теореме о трех перпендикулярах. ОС = а - расстояние от центра сферы до ребра MN.

ΔОВС = ΔОАС (ОВ = ОА = R, ОС - общая) значит, ОС – биссектриса ∠ACB = 120°, значит, ∠OCA = 60°. В ΔОСА: OA = R = 0 sin 60° = ΔАОВ - равнобедренный, (ОВ = ОА = R) ∠AOB = 60°, значит, ∠OBA = ∠OAB = 60°, то есть ΔАОВ - равносторонний АВ = ОА = расстояние между точками касания.

(Ответ: , .)

2. Повторение

а) работа по карточке сфера задана уравнением: x2 + y2 + z2 + 2y - 4z = 4. Найдите координаты центра и радиус сферы.

x2 + y2 + z2 + 2y - 4z = 4 выделим квадрат двучлена: х2 + у2 + 2у + 1 - 1 + z2 - 4z + 4 - 4 = 4, х2 + (у + 1)2 + (z - 2)2 = 9 центр окружности С(0; -1; 2), радиус R = 3.

б) устный опрос учащихся:

1) Что мы называем сферой?

Поверхность, состоящая из множества точек, равноудаленных от центра.

2) Что называется шаром?

Часть пространства ограниченная сферой.

3) взаимные расположения плоскости и сферы:

- нет общих точек;

- пересекаются по окружности;

- касаются (имеют одну общую точку)

4) касательная плоскость к сфере

Плоскость, имеющая со сферой только одну общую точку.

5) уравнение сферы

(x - х0)2 + (у - у0)2 + (z - z0)2 = R.

в) работа с чертежом (устно) (рис. 2)

АВ = 6 см, ВС = 8 см, АС = 10 см.

Найти: ОК.

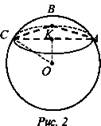
ΔABC прямоугольный, так как 102 = 82 + 62, т.е. ∠CBA = 90°, значит, ∠CBA опирается на диаметр сечения СА, тогда радиус, сечения r = 10 : 2 = 5 (см), К - центр круга, значит, по теореме Пифагора.

г) рассмотрим вопросы из учебника:

№ 7. Точка А и В принадлежат шару. Принадлежит ли этому шару любая точка отрезка АВ?

Да

№ 8. Могут ли все вершины прямоугольного треугольника с катетами 4 см и 2√2 см лежать на сфере радиуса √5?

- диаметр сечения, на который опирается прямой угол, значит, радиус такого сечения что больше радиуса сферы, таким образом, нет, не могут.

№ 9. Могут ли две сферы с общим центром и с неравными радиусами иметь общую касательную плоскость?

Нет.

III. Изучение нового материала

1) Рассмотрим рисунок 156 учебника.

Многогранник называется описанным, если сфера касается всех его граней. Сфера будет вписанной в этой многогранник.

2) Площадью сферы будем называть предел последовательности площадей поверхностей, описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.

S = 4πR2.

IV. Закрепление изученного материал.

№ 593 а)

№ 594

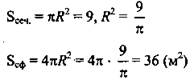
№ 596

пропорциональны.

V. Самостоятельная работа (обучающего характера) (10 мин)

I уровень

Сечение шара площадью S = 16π см2 находится на расстоянии 3 см от центра шара.

Найдите площадь его поверхности.

Дано: шар с центром в точке О, Sсеч. = 16π см2, расстояние от точки О до сечения 3 см (рис. 3).

Найти: Sсф.

Решение: значит, 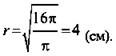Рассмотрим ΔОАВ OA = d - расстояние, значит, ∠A = 90°. (Ответ: 100π см2.)

II уровень

К сфере с S = 64π см2 проведена касательная плоскость. Кротчайшее расстояние от точки А, лежащей в этой плоскости, до данной сферы равно 1 см.

Найти расстояние от точки А до точки касания сферы с плоскостью.

Дано: сфера с центром в точке О, α - касательная плоскость, В - точка касания, А - точка принадлежащая плоскости α, АМ = 1 см, М - точка пересечения АО и сферы (рис. 4).

Найти: АВ.

Решение: (см). В, М - точки, лежащие на сфере, значит, ОМ = OB = R = 4 см. Рассмотрим прямоугольный треугольник ОВА с ∠B = 90° (В - точка касания ОВ = R). (Ответ: 3 см.)

III уровень

Два взаимно перпендикулярных сечения сферы равноудалены от ее центра. При этом центр сферы находится на расстоянии 4√2 см от общей хорды этих сечений, равной 6 см.

Найдите площадь сферы.

Дано: сфера с центром в точке О, АВ ⊥ CD, АВ - диаметр сечения, CD - диаметр сечения MN – общая хорда. MN = 6 см, ОК = 4√2, ОО1 = ОО2 (рис. 5).

Найти: Sсф.

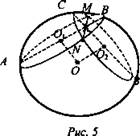
Решение: Рассмотрим прямоугольный ΔONK с ∠OKN = 90°; (Ответ: 164π см2.)

VI. Подведение итогов

Вспомним, по какой формуле вычисляется площадь сферы.

S = 4πR2

Домашнее задание

I уровень. П. 60-62, № 593, 595.

№ 593.

(Ответ: 16π дм2, 8π см2, 48π см2.)

№ 595.

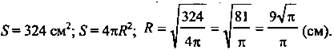(Ответ: см.)

II уровень. № 598, 597, 600.

№ 597. L - радиус круга (Ответ: 10 м.)

№ 598. Дано: сфера с центром в точке О и радиусом R; r1 и r2 - радиусы параллельных сечений сферы, r1 = 9 см, r2 = 12 см, l = 3 см - расстояние между секущими плоскостями (рис. 6).

Найти: Sсф.

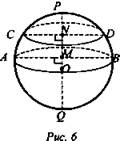
Решение: Проведем диаметры перпендикулярно к данным параллельным сечениям. Через диаметр проведем секущую плоскость, которая пересечет сферу по окружности, радиус которой равен радиусу сферы ND = r1 = 9 см, MB = r2 = 12 см, NM= 3 см, OD = ОВ = R в ΔOВМ: в ΔODN:

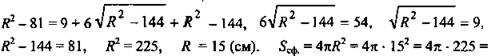
(Ответ: 900π см2.)

№ 600.

Цилиндр получен путем вращения квадрата ABCD вокруг стороны Следовательно,