Поурочные разработки по геометрии 10 класс
Урок 9. Самостоятельная работа обучающего характера - Контрольные и самостоятельные работы - ПРИЛОЖЕНИЯ
I уровен.
Вариант I
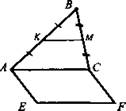
1. Треугольник ABC и квадрат AEFC не лежат в одной плоскости. Точки К и М - середины отрезков АВ и ВС соответственно.
а) Докажите, что КМ || EF.
б) Найдите КМ, если АЕ = 8 см.
2. Плоскость α проходит через основание AD трапеции ABCD. Точки Е и F - середины отрезков АВ и CD соответственно. Докажите, что EF || α.
Вариант II
1. Квадрат ABCD и трапеция KMNL не лежат в одной плоскости. Точки А и D - середины отрезков КМ и NL соответственно.
а) Докажите, что KL || ВС.
б) Найдите ВС, если KL = 10 см, MN = 6 см.
2. Плоскость α проходит через сторону АС треугольника ABC. Точка D и Е - середины отрезков АВ и ВС соответственно. Докажите, что DE || α.
II уровень
Вариант I
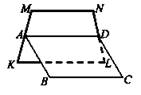
1. Точки А, В, С и D не лежат в одной плоскости. Точки Е, F, М, К - середины отрезков АВ, ВС, CD, AD соответственно.
а) Докажите, что EFMK - параллелограмм.
б) Найдите периметр EFKM, если АС = 6 см, BD = 8 см.
2. Точка А лежит в плоскости α, параллельной прямой а. Через точку А проведена прямая b, параллельная прямой а. Докажите, что прямая b лежит в плоскости α.
Вариант II
1. Точка А не лежит в плоскости треугольника BCD. Точки Р, R, S и T - середины отрезков АВ, AD, CD и ВС соответственно.
а) Докажите, что PRST - параллелограмм.
б) Найдите АС, если BD = 6 см, а периметр PRST равен 14 см.
2. Прямые а и b параллельны. Через точку В, лежащую на прямой b, проведена плоскость α, параллельная прямой а. Докажите, что плоскость α проходит через прямую b.
III уровень
Вариант I
1. Точка М, лежащая вне плоскости ΔАВК, соединена с его вершинами. D и Е - точка пересечения медиан треугольников МАВ и МВК соответственно.
а) Докажите, что ADEK - трапеция.
б) Найдите DE, если АК = 14 см.
2. Отрезки AA1, ВВ1 и СС1 не лежат в одной плоскости и пересекаются в точке О, являющейся серединой каждого из них. Докажите, что прямая АВ параллельна плоскости А1СВ1.
Вариант II
1. Точки А, В, С и D не лежат в одной плоскости. К и М - точки пересечения медиан треугольников ADB и DBC соответственно.
а) Докажите, что КМ || АС.
б) Найдите АС, если КМ = 6 см.
2. Через точку О - точку пересечения диагоналей параллелограмма ABCD - проведена прямая КМ, не лежащая в плоскости ABC, причем О - середина отрезка КМ. Докажите, что прямая КВ параллельна плоскости AMD.